Lesson 9
The subject of the lesson
In this lesson we'll consider the most important outcome of the theory of Complex Numbers, The Fundamental Theorem of Algebra, and we'll treat in detail the case of quadratic equations.
The lesson begins
Exercise: consider the polynomial, in R, p(x) = x2-5x+6. Try to factorize it. [Answer: (x-2)(x-3)]
Exercise: consider the polynomial, in R, p(x) = x3-6x2+11x-6. Try to factorize it. [Answer: (x-1)(x-2)(x-3)]
Exercise: consider the polynomial, in R, p(x) = x4-1. Try to factorize it. [Answer: (x-1)(x+1)(x2+1)]. What is the remarkable difference between this factorization and the previous ones? [Answer: in this case we can't get a factorization in terms of the first degree].
Exercise: consider the polynomial, in
R, p(x) =
x4+1. Try to factorize it. The answer is not
so easy as in the previous examples: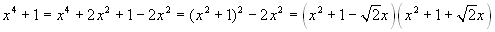 
. The most important
observation is, however, that in this case one can obtain only a
factorization in terms of the second degree.
Exercise: consider the polynomial, in R, p(x) = x3+3x2+3x+1. Try to factorize it. The answer is (x+1)(x+1)(x+1). In this case we have a product of three identical factors, all of the first degree.
We can conclude that, when dealing with the set of real numbers, some polynomials can be factorized only in terms of the first degree, while others cannot.
Exercise: consider the polynomial, in C, p(z) = z4-1. Using the 4-th roots of 1, try to factorize it only in terms of the first degree. As the 4-th roots of 1 are 1, -1, i, -i, we easily get: z4-1 = (z-1)(z+1)(z-i)(z+ i).
The issue of last example is very important and is of general nature: while dealing with the set of Complex Numbers we can always factorize polynomials in terms only of the first degree.
We are mainly interested in polynomials of the second degree: p(z) = az2+bz+c (a, b and c may be complex numbers). With the aid of the well known formula for finding the roots of a quadratic equation, and remembering that every complex number has two differents roots, we immediatly conclude that it is always possible to get a factorization of such a polynomial in terms of the first degree: p(z) =az2+bz+c=(z-z 1)(z-z2).
Try the following exercises.
-
Factorize the polynomial p(z) =
z2-iz+1.
-
.
-
-
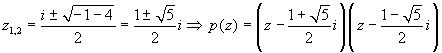Factorize the polynomial p(z) =
z2-2z-i.
-
.
-
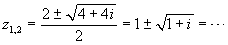The lesson ends - Homework
The search of the square roots of a complex number is possible (and sometimes easier) without using the polar form. In the sheet containing the homework you'll find an example: try to understand it. Tthen use the technique to solve exercises 9 and 10. Download the homework (pdf file).