Lesson 1
The subject of the lesson
In this lesson we're going to solve some second degree
equations in one unknown, showing that some equations have
solutions, while others don't. Then we'll solve some
linear system in two unknowns. All these concepts are very
important in the path to the introduction of the set of complex
numbers.

La chiara esplicitazione dei contenuti e degli obiettivi di
una lezione è, sempre, una necessità
fondamentale: lo diventa tanto di più quando si vuole
utilizzare come strumento di comunicazione una lingua diversa
da quella usuale nella comunicazione quotidiana.
Nascondi questa nota
The lesson begins
If we consider the equation x2-1=0, we can
immediatly find the solutions, that are x=±1. A
slight modification of the equation,
x2+1=0, provides an example of a problem
with no real solution.
This is somewhat cumbersome: two very similar problems have a
completely different behaviour. Mathematicians don't like
this and they have found the way to overcome the problem.
We'll see in the next lesson how this is possible.
Now try to find some other examples of the same kind: an
equation has solutions, while an almost similar one has no
solution.

A questo punto gli studenti sono invitati a ricercare esempi,
venendo a presentarli alla lavagna, discutendo con il docente
e con i compagni le ragioni dei diversi comportamenti. E'
opportuno che gli studenti scrivano le equazioni alla lavagna
e leggano, utilizzando la lingua inglese, quanto scritto.
Nascondi questa nota
Now we are interested in the problem of solving a system of two
equations in two unknowns. If the system is a first degree one,
its solution is straightforward (using for instance a
substitution technique), but if it is a second or higher level
degree, the solution is not always simple. We'll now
consider some examples and try to solve them, in order to bring
to our minds the main techniques.

A questo punto vengono proposti alcuni sistemi di secondo
grado (un'equazione di primo ed una di secondo grado) o
di quarto grado (due equazioni di secondo grado), pensati con
lo scopo di costituire dei modelli per le future applicazioni
alla ricerca delle soluzioni di problemi coinvolgenti i
numeri complessi. Si deve tenere presente che l'argomento
"sistemi di equazioni" è già noto
agli studenti, e qui lo scopo è, da un lato, quello di
richiamare le tecniche coinvolte, dall'altro quello di
acquisire dimestichezza con l'uso della lingua inglese
nel "leggere la matematica". Ci preme anche
segnalare come la parte ex-cathedra della lezione
sia veramente ridotta all'osso e come invece lo studente
sia il protagonista della lezione e, addirittura, della
spiegazione: su una durata complessiva di 50 minuti circa,
non più di 5 sono stati riservati alla
"presentazione" da parte del docente.
A mo' d'esempio riportiamo uno degli esercizi
proposti agli studenti: 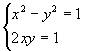 . Segnaliamo che questo esempio viene
proposto avendo in mente la risoluzione, che sarà
trattata più avanti, dell'equazione in
C: z2=1+i.
. Segnaliamo che questo esempio viene
proposto avendo in mente la risoluzione, che sarà
trattata più avanti, dell'equazione in
C: z2=1+i.
Nascondi questa nota
The lesson ends - Homework

Ogni lezione di questo modulo termina con la proposta di
alcuni esercizi da svolgere a casa, a rinforzo dei concetti
appresi. E' bene che gli esercizi proposti non si
discostino molto da quelli svolti in classe e trattati
durante la discussione. Per questo la scelta degli esercizi
da proporre dipende in gran parte dall'andamento della
lezione e dagli interventi degli studenti e non può
essere prevista integralmente "a tavolino". La
soluzione più efficiente a questo problema è
quella di preparare gli esercizi per casa dopo la lezione;
naturalmente questo introduce la difficoltà di come
comunicarli agli studenti. L'ideale sarebbe di poter
disporre di un canale di comunicazione via internet, o
mediante e-mail o mediante la pubblicazione su un sito
raggiungibile pubblicamente o mediante password. La cosa
è possibile solo se si è preventivamente
accertata la possibilità per tutti gli allievi di
avere a disposizione un accesso ad internet. In caso di
impossibilità osserviamo che si possono anche
prelevare esercizi scegliendoli opportunamente da un
qualunque testo, e dettarli agli studenti negli ultimi minuti
della lezione.
Nascondi questa nota
Download the homework (pdf file).
copyright 2000 et seq. maddalena falanga & luciano battaia
first published on april 04 2005 - last updated on april 04 2005
![]()
![]()
![]()
![]()
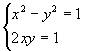 . Segnaliamo che questo esempio viene
proposto avendo in mente la risoluzione, che sarà
trattata più avanti, dell'equazione in
C: z2=1+i.
. Segnaliamo che questo esempio viene
proposto avendo in mente la risoluzione, che sarà
trattata più avanti, dell'equazione in
C: z2=1+i.