Lessons 7 and 8
The subject of the lessons
These are two somewhat difficult lessons; we'll find a surprising outcome: every complex number has exactly n different n-th roots. It is one of the reasons that make this set of numbers very interesting. Remember that, when dealing with real numbers, the situation was very different (for example: positive real numbers have two different quadratic roots, negative real numbers have no quadratic roots, all real numbers have one only cubic root). We'll be especially interested in the roots of the (complex) number 1 (that is 1+0i). Pay the greatest attention to the explanation that will be longer than usual.
The lessons begin
Consider a complex number in its polar form: u = [ρ,θ]. From the multiplication rule we can immediately deduce that the nth power of the number is un = [ρn,nθ]. This simple formula is called De Moivre's formula.
Now consider the problem of finding the roots of a given complex
number: the definition of an n-th root is the same
already considered while dealing with real numbers: a complex
number u is an n-th root of the complex
number z if un = z. If we consider
the polar form of z, [r,α], first of all
we get: ρn = r, that is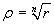 
.
Besides this we observe that we can have not only nθ = α, but also nθ = α+360°, or nθ = α+2·360°, or nθ = α+3·360°, and so on: in fact while adding 360°, or its multiples, you do not change the point in the Gauss plane. It is not difficult to find that it's enough to consider only the multiples of 360° up to n-1, in order to obtain all points in the Gauss plane that satisfy the requirings.
So we can conlcude with the following rule.
Given a complex number z = [r,α] the
numbers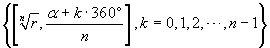 
are the n-th roots of z,
and are denoted by 
.
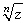Examples
Download the examples (pdf file).
A very important consequence you can deduce from the examples
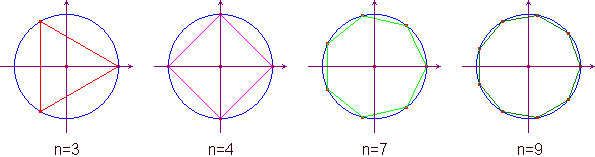
above is the one concerning the n-th roots of 1. For
every n you get: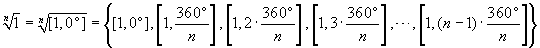 
. This means that all the roots are placed
on the unit circumference centred in the origin of the axes, at
the vertices of a regular polygon with a fixed point in (1,0).
See the following picture for some examples.
The lessons end - Homework
Download the homework (pdf file).