Lesson 10
The subject of the lesson
In this lesson we're going to give some definitions to complete our introduction to the set of Complex Numbers and then we'll solve some exercises as a training to next classwork.
The lesson begins
![]()
Some definitions and properties.
Complex conjugate: given a complex number
z=a+ib, the number a-ib is called its
coonjugate and denoted by: ![]() .
.
Real part: given a complex number z=a+ib, the number a is called its real part and denoted by Re(z).
Imaginary part: given a complex number z=a+ib, the number b is called its imaginary part and denoted by Im(z).
Argument: given a complex number z=a+ib=[ρ,θ], the number θ is called its argument and denoted by arg(z).
Absolute value: given a complex number z=a+ib=[ρ,θ], the number ρ is called its absoulte value, or modulus, and denoted by |z|, as with real numbers.
For every complex number z we have Re(z) =
(z + ![]() )/2 and Im(z) = (z -
)/2 and Im(z) = (z - ![]() )/2.
)/2.
For every complex number z we have 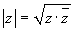 .
.
Final exercises
Downlaod the exercises (pdf file).
Conclusion
This is the last lesson of our short introduction to the set of Complex Numbers. As a training to the classwork you can use all the sheets of exercises given so far and try to solve by yourselves the exercises used as examples during classes.