Lesson 2
The subject of the lesson
In this lesson we are going to introduce the trick cooked up by mathematicians in order to solve "impossible equations", such as x2+1=0. We'll find that the solution is very simple and that here is substantially one only new math rule to know.
The lesson begins
The reason that prevents the equation x2+1=0 from having solutions is that there is no real number x whose square is -1: the square of every real number is, in fact, greater than zero. So the idea to circumvent this problem is: can we consider a new, imaginary, object (not yet a number!), that we can call i (the first letter of imaginary), whith the property that i2=-1?
Let's suppose that this is possible and try to make some calculations, treating this object as an ordinary number, with the extra property that i2=-1 and preserving all other properties already known: we'll find that this is the right idea!
![]()
Exercise 1: Find i3, i4, i5, and so on up to i10. Can you conclude something interesting about the subsequent powers of i?
Exercise 2: How can we write i+i?
Exercise 3: How can we write 2i+5i?
Exercise 4: Is there a simpler way of writing 2+i?
Exercise 5: How can we simplify the addition of 3+2i and 5-4i?
Exercise 6: How can we write the product of 3+2i and 5-4i?
Exercise 7: How can we write the quotient of 3+2i and 5-4i?
![]()
Exercise 8: Try to simplify the following
expression: 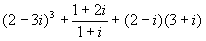 .
.
Conclusion
Having introduced the "object" i with the strange property that i2=-1, we have obtained a whole category of new objects that can be written in the form a+ib, where a and b are real numbers. With these objects we can do the operations as with ordinary real numbers and all properties of the operations are still valid. We'll see that this is the central point in our construction of Complex Numbers.
The lesson ends - Homework
Download the homework (pdf file).