Examples of linear systems
1 - Solve the system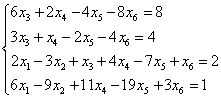 
.
The augmented matrix A|b of the system is: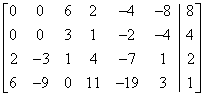 
,
which is row equivalent to the reduced row-echelon matrix
B|c: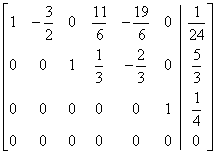 
.
The solution of the system is easily found: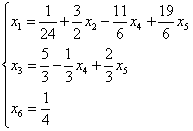 
. The other unknowns are completely arbitrary. This
system has n=6, m=4, r=3, and so
∞6-3=∞3 solutions.
2 - Solve the system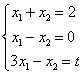 
, where t is a real number.
The augmented matrix and its reduced form are: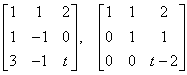 
. The system is consistent if and only if t=2.
In this case the reduced row-echelon form of the matrix is: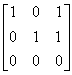 
. We read off the unique solution of the system:
. From a geometrical point of view this
result can be interpreted as follows: given two non parallel
straight lines and a third variable straight line, find the
value of t for which this third line has a unique point
in common with the preceding two.
3 - Solve the system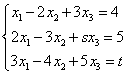 
, where s and t are real
numbers.
Write the augmented matrix A|b: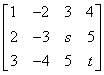 
.
Now start applying Gauss-Jordan algorithm.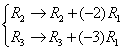 
; 
.
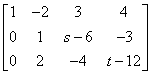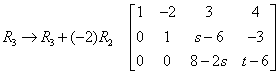Now we must distinguish between to cases:
-
If s≠4 the system has only one solution
that we found proceding from bottom to top: we begin finding
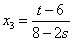, then we find the second unknown
using the second equation and finally the first unknown using
the first equation. There is no need to produce the reduced
row-echelon form of the matrix.
-
If s=4 we must check the value of t.
- If t≠6 the system is inconsistent.
-
If t=6 we produce the following matrix:
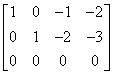. We can easily read off the
solution: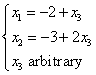 
.