Fundamental theorem of the integral calculus
The integral function F and the integrand function f give an example of two functions with F'=f. In general we give the following
If f is a function whose domain is an interval I of real numbers, we call antiderivative of f every function F such that, for all x in I, the following property holds: F'=f.
For example sinx is an antiderivative of cosx, as (sinx)'=cosx.
Observe that F is an antiderivative if the property F'=f holds for every x in I. So antiderivative is a set property, and it makes no sense to speak of antiderivative in a point.
In this site ou can find a complete study of the concept of antiderivative
(in Italian). Here we only remind that a special symbol is used
to represent the set of all antiderivatives of a given function
f: 
or 
or 
, that is almost the same symbol used
for the Riemann integral, without the bounds. But pay attention:
these symbols represent a set of functions, not a real number!
Continuity of the integral function
The integral function of a given function f is always more regular than f. The following theorem concerns its continuity.
Theorem
The integral function of a Riemann integrable function is
always continuous. 
Let's consider an example using the integral part function
(this is a step function, so its integral is very simple). It is
not difficult to prove that, in the interval [-3,3[, we have:
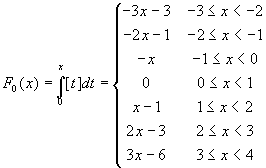. In order to do this observe that, for
positive x you must calculate the yellow area in the
picture below on the left, for negative x the green
area. In the picture below, on the right we have represented
this integral function.
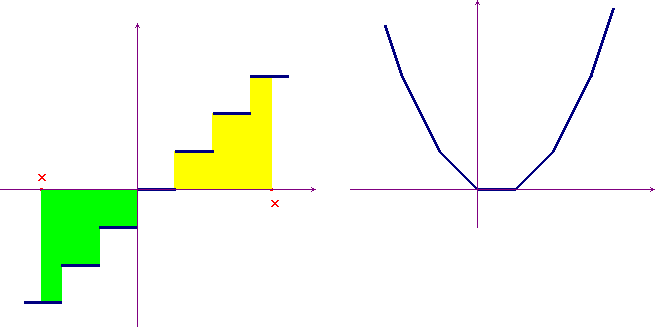
The fundamental theorem of integral calculus
The following theorem, as its name shows, is one of the most important outcomes of analysis. It allows us to calculate, by a very simple technique, a wide class of integrals, without using a direct calculation based on the definition.
Theorem
If an integrable function 
is continuous in a
point d, then the integral functions, with starting
point each number c of [a,b], are
differentiable in d, and
Fc'(d)=f(d).
The main consequence of this theorem is that if a function is continuous in an interval [a,b], the integral functions with starting points all points in [a,b] are antiderivatives of f (however in this way we do not obtain all the antiderivatives of f, as we'll see): so continuous functions have always antiderivatives.
This theorem is known as the Torricelli-Barrow theorem.
Examples
-
The function
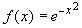is continuous
everywhere. As a consequence the functions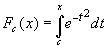 
are differentiable functions, and 
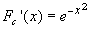, so they are also monotòne increasing
functions. These functions are not elementary functions:
there is no way to represent them by means of a finite number
of sums, multiplications, divisions on the independent
variable, nor by means of functions such as exponentials,
logarithms, trigonometric functions. The proof of this fact,
however, is not easy at all, and is far beyond the limits of
this presentation of the Riemann integral.
-
The same considerations apply to the function
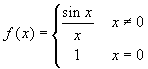whose integral functions are not elementary functions.
However they are differentiable and their derivative is
always f(x).
-
Considering again the function
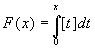, its easy to prove that it is differentiable
everywhere, except at the points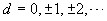 
, where the function [x] is not continuous. At all
points where the function is differentiable the equality
F'(x)=[x] holds.
Calculation of integrals
We'll now show how, using the fundamental theorem, one can easily calculate Riemann integrals, provided an antiderivative is known.
Let G(x) be an antiderivative of a continuous function
, then as 
is also an antiderivative, we must have 
.
But 
and 
.
We may conclude that 
. This equality is
usually written as 
.
This result is summarized by the following
Theorem
If G(x) is an antiderivative of a continuous function
, then .
This theorem is sometimes called The second fundamental theorem of integral calculus: if you know an antiderivative of a continuous function, the calculation of the Riemann integral is only a matter of substitution!