Some properties of the Riemann integral
The same properties already considered for the integral of step functions remain unchanged for the Riemann integral. Their proof is not difficult: in some cases it can be obtained by simple generalisation of the same property for the integral of step functions, in other cases it is a simple consequence of the Vitali-Lebesgue theorem.
-
Linearity property. If two functions
f and g are integrable on the same interval
[a,b], then any linear combination of the two is
also integrable and
.
-
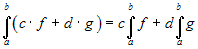Additive property with respect to the integration
interval. Given three numbers a, b
and c (whose order is unimportant), and a function
f,
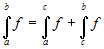, provided the function
is integrable in each of the intervals considered.
-
Comparison property. Given two functions
f and g that are integrable on the same
interval [a,b] (with a
< b), if
f(x)≤g(x) for all x in [a,b] then: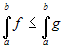
.
- Product and quotient property. If two functions are integrable, also their product is integrable. The quotient of the two functions is integrable, provided it is bounded.
-
Absolute value property. If a function
f is integrable, also its absolute value is
integrable and the following inequality holds (a
< b):
.
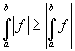Observations
The linearity property can obviously be generalized to any
finite number of functions as follows: if
f1, ... , fn are
functions integrable on the same interval [a,b], then
c1f1 + ... +
cnfn is also integrable and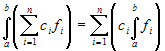 
, for any choice of the constants
c1, ... , cn.
Observe that if two functions are not integrable, their sum may be integrable: it's enough to take a non integrable function and the opposite one, so the sum is zero. The same holds for the product and the quotient of two non integrable functions.
The comparison property has an important consequence: setting
f(x)=0 you obtain 
, if
g(x)≥0: the Riemann integral of a positive
function is positive. The converse is not true: if the integral
of a function is positive, the function is not necessarily
positive. A simple example can be given using the function
signum (as this is a step function its integral is easy
to calculate): we have 
, but the function
is not positive in the interval [-1,2].
As far as the absolute value property is concerned observe that
the converse of the property is not true: the absolute value of
a function may be integrable, while the function is not.
Consider for example 
, whose absolute value is
a constant function.