Playing with Gauss: a software to solve linear systems of m equations in n unknowns
The program you can reach following the links above solves a linear system of m equations in n unknowns, using the Gauss-Jordan algorithm, that is a process that, starting with a given matrix A, produces a row-echelon reduction, B, of the same matrix. The reduced matrix B will be a much simpler matrix from which the consistency or inconsistency of the corresponding linear system is immediately apparent.
The software is suitable for systems with a maximum of ten equations and ten unknowns, in order to prevent typical overflow problems.
You must first decide the number of equations and unknowns, then you'll be asked to introduce the coefficients. Only rational coefficients are allowed, in the form: (-)numerator(/)denominator, where the brackets mean optional objects. Only natural numbers are allowed for numerators and denominators.
After typing in all the coefficients you must press the appropriate button and the program cheks the inputs. If needed a reduction of fractions is operated.
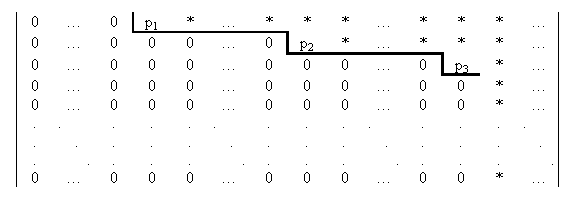
Now it is possible to procede in the solution, keeping in mind that the required row-echelon form of the coefficient matrix must be as in the following picture:
,
Obviously the process applied to the coefficient matrix affects also the augmented matrix. The non-zero numbers p1, p2, etc are the pivots: they are the leading numbers of each non-zero row; all zero rows (if any) are at the bottom of the matrix and if two successive rows are non-zero, the second starts with more zeros than the first (moving from right to left).
The number of pivots is called the rank, r, of the system. It is not difficult to see that the system is consistent if and only if the augmented matrix of the system, after the application of the Gauss-Jordan algorithm, has zero coefficients in correspondance with the m-r zero rows (if any) of the reduced coefficient matrix. If the system is consistent we shall say that it has ∞ n-r solutions (∞ 0, in this convention, means 1).
The solution requires the following steps:
-
Find the first non-zero column moving from left to right (usually there are no zero columns, otherwise the corresponding unknown is useless, but it is better to consider this more general case).
-
By interchanging rows, if necessary, ensure that the first entry in this column is non-zero: this leading entry is the first pivot, p1.
-
With suitable linear combinations we proceed in order to obtain all zeros "under" this pivot. The method is the following: if the row number i has a non zero element, a, we multiply row 1 by
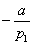and add it to row i.
-
Repeat the process to the matrix under row 1.
The program presented here uses exactly this method, and requires the intervention of the user at all steps: the only automatic operation is the calculation of the multiplier required for the linear combination. Once the row-echelon form is obtained the program can solve, if requested, the system.
Sometimes problems of overflow can arise, especially for systems with many equations or unknowns: this is due to Javascript's inability to use integer numbers with more than 15 digits. So you are asked to careful check the solutions.
Only for laziest people there is also a completely automatic version of this code.