Relatività e campo elettromagnetico
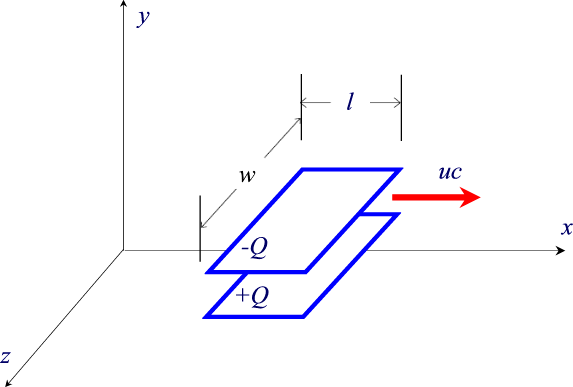
Consideriamo un condensatore piano mobile, in un dato
riferimento, con velocità v. Siano
l0 e w0 le sue
dimensioni misurate da un osservatore solidale al condensatore
(dimensioni a riposo). Poniamo, per questioni di
semplicità, u=v/c (ciò equivale a
misurare le velocità in "unità c");
avremo dunque v=uc. Le dimensioni misurate da un
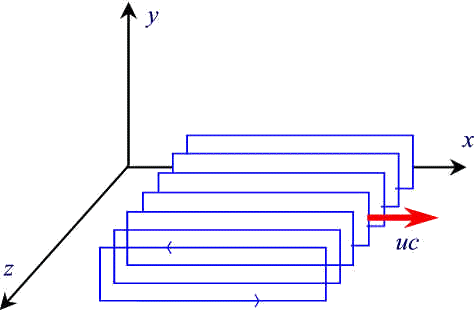
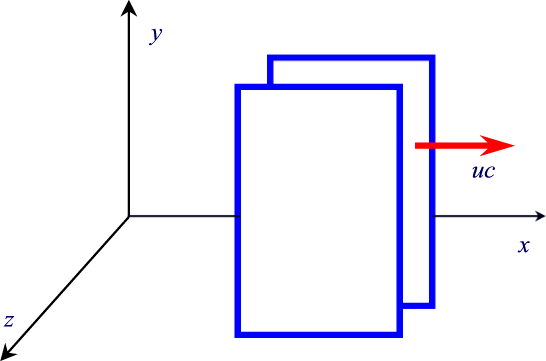
osservatore solidale al riferimento saranno 
e w=w0. Supponiamo che le due
piastre siano caricate come nella figura qui sotto. Tra le
due piastre è presente un campo elettrico, uniforme,
diretto nel verso positivo dell'asse y e dato dalle formule:
.
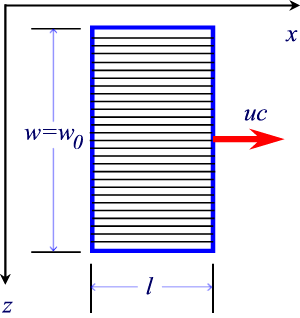
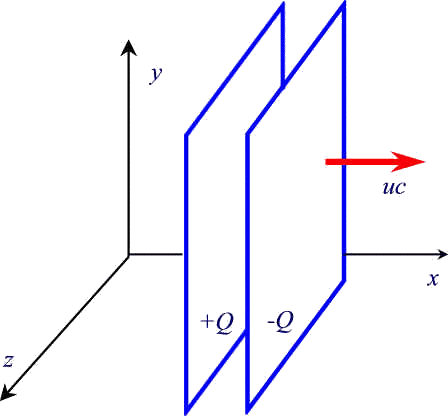
Le due piastre in movimento costituiscono delle correnti e dunque generano un campo magnetico. Se supponiamo di dividere ognuna delle due piastre in tante striscioline parallelamente alla direzione del movimento, come nella figura qui sotto dove abbiamo rappresentato la situazione vista dall'alto, potremo pensare ad ognuna delle due piastre come ad un insieme di fili percorsi da corrente, messi vicinissimi uno all'altro.
Se N è il numero di suddivisioni, cioè di fili percorsi da corrente, la piastra negativa sarà percorsa da correnti nel verso negativo dell'asse x, quella positiva da correnti nel verso positivo.
Il condensatore sarà assimilabile ad un solenoide se
immaginiamo che ciascun filo sulla piastra negativa si chiuda a
circuito con il corrispondente della piastra positiva.
Come in un normale solenoide all'interno sarà presente un campo magnetico, uniforme, diretto nel verso positivo dell'asse z, e dato dalle formule (n rappresenta, al solito, il numero di spire per unità di lunghezza):
.
Per valutare la corrente i possiamo utilizzare il seguente
ragionamento: la carica Q contenuta su ognuna delle
piastre si sposta, verso la direzione positiva dell'asse x,
del tratto l nel tempo 
. La carica, q, contenuta su ognuna delle
suddivisioni è 
, dunque la corrente i è data da
. Per il campo B
si ottiene, tenendo anche conto che
w=w0: 
.
Supponiamo ora di avere un secondo riferimento, mobile con
velocità V nella direzione positiva
dell'asse x. Allora il condensatore avrà una diversa
velocità ,v', in questo riferimento e, se
poniamo 
e 
, per i campi elettrico e magnetico misurati da
questo nuovo osservatore varranno le stesse formule ottenute
prima, con la semplice sostituzione di u' al posto
di u:
.
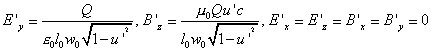Possiamo ora utilizzare la formula per la composizione delle
velocità; dividendo ambo i membri per c, essa
diventa 
. Se sostituiamo questa
formula in quella che dà E' e
B' e ricordiamo che 
, troviamo: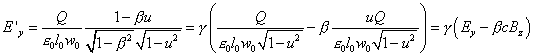 
. In modo perfettamente analogo, se si lavora su
B'z, si ottiene 
.
Se riprendiamo in considerazione il condensatore in moto e lo
disponiamo come nella figura qui sotto, ritroveremo risultati
simili a quelli già visti, ma coinvolgenti ora le
componenti Ez e By dei
campi. Si trova, in maniera quasi identica,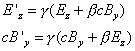 
.
Se disponiamo il condensatore come nella figura qui sotto, otteniamo che Ex=E'x. Si può capire facilmente che il campo elettrico per i due osservatori non è diverso in questo caso perché l'unica cosa che varia da un osservatore all'altro è la distanza tra le piastre, ma il campo elettrico di un condensatore non dipende dalla distanza tra le piastre.
Non è agevole dimostrare che, per il campo magnetico, vale la relazione Bx=B'x, al passaggio da un osservatore ad un altro, nonostante la apparente semplicità della formula, e rinunciamo a proporre i calcoli. Riassumendo le formule che abbiamo via via trovato otteniamo le formule per la trasformazione dei campi da un riferimento all'altro:
.
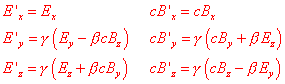Occorre sottolineare che i discorsi che abbiamo fatto per ottenere queste formule non ne costituiscono una dimostrazione rigorosa: sono piuttosto da interpretare come una illustrazione, peraltro molto significativa, di come le trasformazioni di Lorentz intervengono nel cambiamento del campo elettromagnetico da un osservatore all'altro.
Quello che è importante in queste trasformazioni è
che esse miscelano i campi tra loro: non ha senso parlare di
campo elettrico o di campo magnetico, nemmeno in condizioni in
cui, come nell'esempio qui considerato, non intervengano
né fenomeni di induzione né le correnti di
spostamento, quello che conta è il campo
elettromagnetico. Se per esempio ho una carica in quiete nel
primo riferimento avrò un campo elettrico come quello
previsto dalla legge di Coulomb 
e nessun campo magnetico. Nel secondo riferimento
avrò un campo elettrico 
, e quindi non molto diverso dal precedente almeno
per basse velocità, ma avrò anche un campo
magnetico, 
, piccolo per
piccole velocità quando γ
1 e
β0, ma non nullo. Questo fatto
naturalmente era già noto nella teoria classica,
perché una carica in moto genera un campo magnetico, ma
l'apparire ora di questo campo magnetico non è una
cosa strana, è semplicemente una manifestazione del fatto
che i due campi elettrico e magnetico sono espressioni di
un'unica entità fisica: il campo elettromagnetico.
Vedere l'uno o l'altro è solo una questione di
sistemi di riferimento. La unificazione profonda dei concetti di
campo elettrico e magnetico è uno dei pilastri della
teoria della relatività, che, in realtà, si
caratterizza proprio per tutta una serie di unificazioni (spazio
e tempo, energia e momento, campo elettrico e campo magnetico).
É facile risolvere, alla luce delle formule di trasformazione per il campo elettromagnetico, un famoso "paradosso" della teoria classica delle interazioni magnetiche.
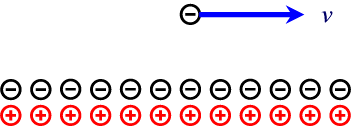
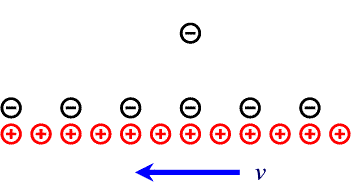
Consideriamo un filo percorso da corrente i nel verso delle x negative, come nella figura qui sotto, e supponiamo di piazzare una carica q, negativa, ad una distanza data dal filo e in moto, rispetto al filo, con la stessa velocità v degli elettroni di conduzione (di norma intorno a 10-4 m/s). Nel riferimento del filo la carica risentirà di una forza, la forza di Lorentz, che la farà avvicinare al filo. Nel riferimento della carica, dal punto di vista classico, nulla cambia per il campo magnetico (invece di cariche negative che si muovono "verso destra" avrò cariche positive che si muovono "verso sinistra" e cioè la stessa corrente di prima), solo che ora la carica è ferma e dunque non ci saranno effetti magnetici. La carica sembra non risentire più di alcuna attrazione verso il filo (si noti che le velocità in gioco sono estremamente basse).
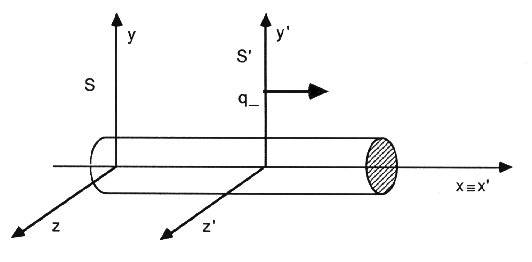
Se descriviamo l'esperimento in termini delle formule di
trasformazione del campo elettromagnetico troveremo che, nel
riferimento del filo, la carica risente di un campo magnetico
avente unica componente Bz data dalla nota
espressione del campo di un filo rettilineo percorso da
corrente, mentre nel riferimento della carica risentirà,
oltreché della presenza di un campo magnetico quasi
uguale a prima, anche della presenza di un campo elettrico
diretto come l'asse y positivo e dato dalla formula 
, che dunque attirerà la carica
negativa verso il filo. (Il fatto che la carica si avvicini al
filo deve essere una proprietà invariante,
cioè indipendente dal riferimento).
Ci si può rendere conto di quanto appena osservato anche con un ragionamento basato solo su misure di lunghezza. Se, nel riferimento del filo, le cariche positive e negative si bilanciano in quanto distribuite allo stesso modo (non c'è effetto elettrostatico prodotto da un filo percorso da corrente), nel riferimento della carica le cariche positive sono viste muoversi verso sinistra, per cui esse risulteranno distribuite su una lunghezza più piccola e non ci sarà più bilanciamento rispetto a quelle negative.
