Quadrilateri inscrittibili o circoscrittibili ad un cerchio
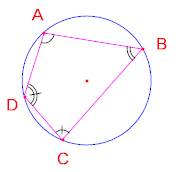Un quadrilatero convesso è
inscrittibile in un cerchio se e solo se gli
angoli opposti sono supplementari: 
.
Un
quadrilatero convesso è circoscrittibile ad
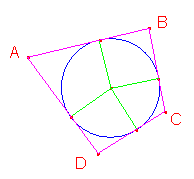un cerchio se e solo se la somma delle due coppie di lati opposti
è uguale: AB + CD = AD + BC.
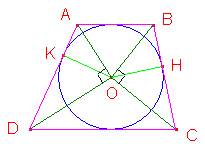Trapezio circoscritto ad un cerchio: i
triangoli BOC e AOD sono rettangoli e la loro
altezza relativa all'ipotenusa è il raggio del cerchio
inscritto.
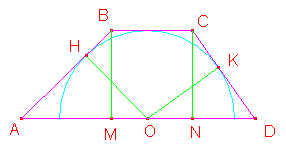Trapezio circoscritto ad un
semicerchio: i triangoli rettangoli ABM e
AOH sono uguali; lo stesso vale per i triangoli
CND e OKD. Ne segue che la base maggiore è
la somma dei lati obliqui.
...
Euclide geomètra e Tolomeo,
...
D.C. 1, IV, 142
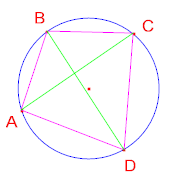Teorema di Tolomeo: in un quadrilatero
convesso inscritto in una circonferenza il prodotto delle
diagonali è uguale alla somma dei prodotti dei lati
opposti:
AC·BD = AD·BC + AB·DC
Teorema di Legendre: in un quadrilatero convesso inscritto in una circonferenza il rapporto delle diagonali è uguale al rapporto delle somme dei prodotti dei lati che concorrono negli estremi delle rispettive diagonali
.