Triangoli rettangoli
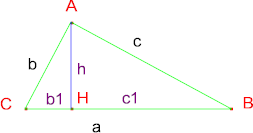Teorema di Pitagora: a2 =
b2 + c2, ovvero il quadrato costruito
sull'ipotenusa è la somma dei quadrati costruiti sui
cateti.
Teorema di Euclide-1: b2 = b1·a, c2 = c1·a, ovvero il quadrato costruito su un cateto è equivalente al rettangolo che ha per lati l'ipotenusa e la proiezione del cateto sull'ipotenusa; o ancora un cateto è medio proporzionale tra l'ipotenusa e la sua proiezione sull'ipotenusa.
Teorema di Euclide-2: h2 = b1·c1, ovvero il quadrato costruito sull'altezza relativa all'ipotenusa è uguale al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa; o ancora l'altezza relativa all'ipotenusa è media proporzionale tra le due proiezioni dei cateti sull'ipotenusa.
...
non si est dare primum motum esse,
o se del mezzo cerchio far si puote
triangol sì ch'un retto non avesse.
D.C. 3, XIII, 100-102
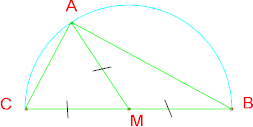Inscrivibilità in una
semicirconferenza: Un triangolo rettangolo si
può sempre inscrivere in una semicirconferenza;
di conseguenza la mediana relativa all'ipotenusa
è la metà dell'ipotenusa ed è il raggio
del cerchio circoscritto.
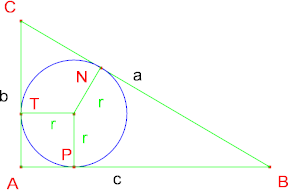Raggio del cerchio inscritto: Il raggio
r del cerchio inscritto in un triangolo
rettangolo è dato dalla formula: 
.