Il teorema di Brianchon e le coniche tangenti a 5 rette
In questa pagina vogliamo esaminare come si possa utilizzare il teorema di Brianchon sulle coniche per costruire una conica tangente a 5 rette assegnate, come luogo inviluppo di una sesta tangente alla conica stessa.
Questo teorema, pubblicato da Charles Julien Brianchon (1783,1864) nel 1806 sul Journal de l'École polytecnique di Parigi, è il duale del teorema di Pascal e afferma
Considerato un esagono circoscritto a una conica, i cui vertici consecutivi sono \(T_{12}, T_{23}, T_{34}, T_{45}, T_{56}, T_{61}\), le congiungenti delle tre coppie di vertici opposti, \(T_{12}\) e \(T_{45}\), \(T_{23}\) e \(T_{56}\), \(T_{34}\) e \(T_{61}\), si incontrano in uno stesso punto.
La figura seguente illustra la situazione nel caso di un'ellisse.
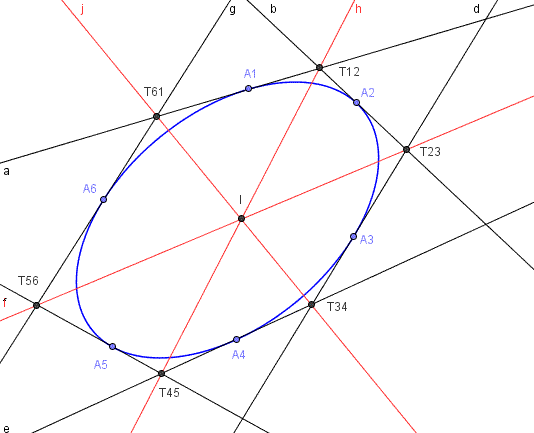
Puoi anche visualizzare un'immagine dinamica della costruzione relativa al teorema di Brianchon.
Qui vogliamo vedere come si possa utilizzare il teorema di Brianchon per costruire una conica tangente a 5 rette date, utilizzando la seguente idea: date 5 rette a cui la conica deve essere tangente, si individua la sesta retta atta a costruire l'esagono circoscritto alla conica stessa. Variando la posizione di questa sesta tangente si otterrà, come inviluppo di rette, la conica richiesta.
Lo schema dei passaggi da eseguire è il seguente.
- Consideriamo i punti \(T_{12}, T_{23}, T_{34}, T_{45}, T\) e costruiamo le rette passanti per due punti consecutivi: i punti \(T_{12}, T_{23}, T_{34}, T_{45}\) saranno i primi quattro vertici dell'esagono circoscritto alla conica, mentre gli altri due vertici saranno determinati dall'algoritmo che segue.
- Tracciamo la retta che congiunge i punti \(T_{12}\) e \(T_{45}\): ad essa dovrà appartenere il punto \(I\) di intersezione delle rette che congiungono le tre coppie di vertici opposti.
- Prendiamo dunque un punto I sulla retta appena tracciata e costruiamo le rette che congiungono \(T_{23}\) e \(T_{34}\) con \(I\).
- I punti \(T_{56}=T_{23}I\cap TT_{45}\) e \(T_{61}=T_{34}I\cap TT_{12}\) individuano una retta che è la sesta tangente alla conica, per il teorema di Brianchon. Facendo variare \(I\) su \(T_{12}T_{45}\) otterremo tutte le posizioni di questa sesta tangente e quindi, per inviluppo, la conica cercata.
La figura seguente illustra i passi indicati.
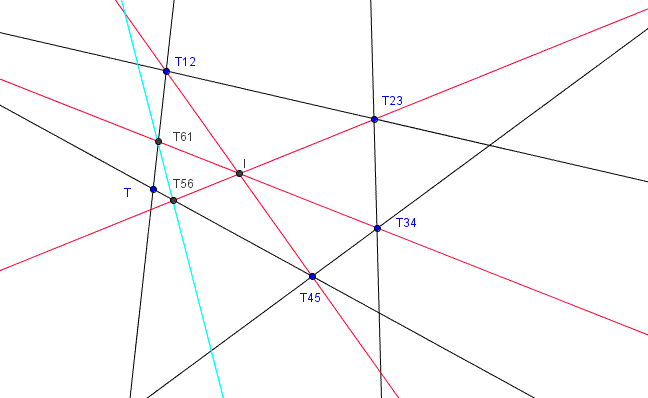
Puoi anche vedere un'animazione della costruzione della conica.