La somma delle radici n-esime dell'unità
Le radici \(n\)-esime dell'unità, nel campo complesso, hanno molte interessanti proprietà. Qui vogliamo porre l'attenzione sul fatto che la loro somma, per ogni \(n\) fissato, è nulla. La cosa si può provare algebricamente, per calcolo diretto, ma ci pare molto più interessante la dimostrazione geometrica che qui vogliamo proporre.
Costruite le \(n\) radici e i loro vettori rappresentativi, basta fare la somma di questi \(n\) vettori per verificare che la loro somma è nulla. La cosa è molto semplice se si usa la regola del "testa-coda": si trasportano successivamente i diversi vettori, nell'ordine e a partire dal secondo, sulla punta del precedente, come evidenziato nella figura che segue, riferita al caso \(n=5\). La costruzione è elementare e non richiede spiegazioni ulteriori.
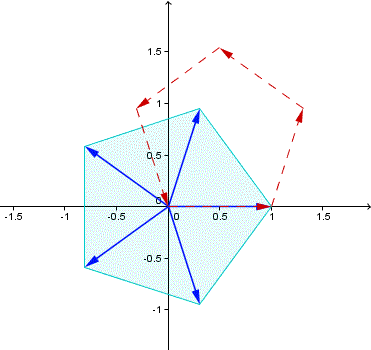
Puoi anche visualizzare una versione dinamica di questa figura, costruita con Geogebra.