La curva simmetrica rispetto a una retta del grafico di una funzione
L'idea di questa costruzione nasce da una discussione sul forum di Geogebra. Al di là dell'interesse specifico per Geogebra, in un forum come questo si possono trovare molte idee e spunti interessanti per l'attività didattica.
In tutti i software di geometria dinamica è presente la macro costruzione del simmetrico di un oggetto rispetto a una retta. Questa macro costruzione di solito non funziona con il grafico di una funzione e la cosa per due ben giustificati motivi.
- Il grafico di una funzione è un "oggetto" un po' speciale: per esempio una circonferenza è individuata semplicemente dal suo centro e dal suo raggio (o da tre suoi punti), un poligono dall'insieme dei suoi vertici, una parabola dal suo fuoco e dalla sua direttrice (o da cinque suoi punti), ecc.: il software può "memorizzare" questi oggetti semplicemente salvando le coordinate di alcuni punti ed eventualmente qualche numero come il raggio di una circonferenza, rendendo molto facile la costruzione dell'oggetto simmetrico. Il grafico di una funzione è individuato da un insieme (in genere enormemente grande) di coppie \(\big(x,f(x)\big)\) di suoi punti, e la possibilità di costruire l'insieme simmetrico dipende chiaramente da come il software "memorizza" questo insieme.
- La curva simmetrica rispetto a una retta della curva grafico di una funzione non è, in generale, il grafico di una funzione.
Vogliamo qui proporre una possibile soluzione a questo problema, soluzione che ci pare di per sé interessante come esercizio di geometria analitica.
Siano allora \(P=(\alpha,\beta)\) un punto del piano e \(r\colon ax+by+c=0\), una retta dello stesso piano, ovviamente con \(a^2+b^2\neq 0\). Il punto \(Q=(\gamma,\delta)\) simmetrico di \(P\) rispetto a \(r\) è caratterizzato dalle seguenti due condizioni:
- il punto medio \(M\) del segmento \(PQ\) appartiene alla retta \(r\);
- il vettore \(\overrightarrow{PQ}\) è ortogonale alla retta \(r\).
La prima è una semplice condizione di appartenenza del punto \[M=\left(\frac{\alpha+\gamma}{2}\,,\,\frac{\beta+\delta}{2}\right)\] alla retta \(r\); per esplicitare la seconda si può osservare che \(\vec{n}=(a,b)\) è perpendicolare alla retta e quindi deve essere parallelo a \(\overrightarrow{PQ}=(\gamma-\alpha,\delta-\beta)\). Scrivendo le condizioni e semplificando si perviene al seguente sistema di due equazioni nelle due incognite \(\gamma\) e \(\delta\), di facile risoluzione con Cramer, per la condizione \(a^2+b^2\neq 0\): \[\left\{\begin{array}{l}b\gamma-a\delta=b\alpha-a\beta\\a\gamma+b\delta=-a\alpha-b\beta-2c\end{array}\right..\]
Si trova:\[\gamma=\frac{b^2\alpha-a^2\alpha-2ab\beta-2ac}{a^2+b^2}\,,\qquad\delta=\frac{a^2\beta-b^2\beta-2ab\alpha-2bc}{a^2+b^2}\,.\]
La costruzione di una figura con geogebra può ora procedere con i seguenti passi.
- Costruire tre numeri (che indicheremo con \(a,b,c\)), per esempio mediante tre slider, così sarà possibile variarli dinamicamente;
- assegnare una funzione (per esempio \(f(x)=\sin x\)): i punti del grafico di questa funzione saranno del tipo \((t,f(t))\), con un opportuno insieme di variabilità del parametro \(t\);
- mediante lo strumento Curva costruire una curva in cui la prima espressione è il valore di \(\gamma\), la seconda espressione il valore di \(\delta\), avendo cura di mettere al posto di \(\alpha\) il parametro \(t\) e al posto di \(\beta\) il valore \(f(t)\); naturalmente \(t\) sarà il nome del parametro e dovremo scegliere opportunamente i valori iniziale e finale;
- volendo si potrà naturalmente costruire anche l'asse di simmetria.
La figura che segue illustra una costruzione relativa alla funzione seno.
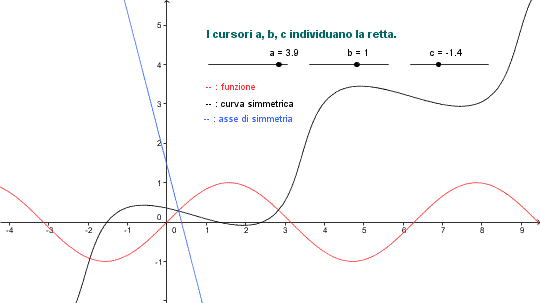
Puoi anche visualizzare una versione dinamica di questa figura, costruita con Geogebra.