www.batmath.it

Ricerca numeri perfetti

Un numero si dice perfetto se è uguale alla somma dei suoi divisori, escluso se stesso. I primi quattro numeri perfetti (6, 28, 496, 8128) erano già noti ai greci. Il quinto (33.550.336) si trova in un manoscritto medioevale anonimo. I due successivi (8.589.869.056 e 137.438.691.328)  furono scoperti dal matematico Bolognese Pietro Antonio Cataldi, nel 1588.

Ci sono molte cose interessanti relativamente ai numeri perfetti, tra cui per esempio il fatto che non è stato ancora scoperto alcun perfetto dispari, anche se, per ora, non si può escludere che ce ne siano. Gli interessati possono effettuare anche una ricerca sulla rete dove si trova una quantità impressionante di materiale su questo argomento. Qui ci preme segnalare un fatto interessante dal punto di vista informatico: l'algoritmo elementare per la ricerca dei numeri perfetti non è in grado di scoprire, in tempi ragionevoli, alcunché di nuovo rispetto alle conoscenze dei greci. Se, per esempio, si volesse provare ad usare questo programma per cercare il quinto numero perfetto, bisognerebbe impostare un intervallo di ricerca almeno tra 8129 e 100.000.000: non abbiamo fatto il tentativo, ma probabilmente 24 ore di calcolo non sarebbero sufficienti!! Esiste anche una "scorciatoia", almeno per i perfetti pari: si tratta di un teorema la cui idea di base è dovuta ad Euclide e che fu poi dimostrato completamente da Eulero (ogni numero perfetto pari è della forma , ove il numero tra parentesi è un numero, detto di Mersenne, primo). 

Tutto il lavoro in javascript è fatto dalla funzione qui sotto, dove abbiamo messo in grassetto la parte importante del codice; il resto è controllo dell'input (all'inizio) e ordinamento dei divisori per la stampa (nella seconda metà). Per velocizzare un po' il calcolo abbiamo fatto la seguente osservazione: se d è un divisore di un numero n, più grande della radice quadrata di n, allora , cioè n/d è un divisore minore della radice di n. Allora se troviamo un divisore d₁ minore della radice di n, basterà aggiungere all'elenco dei divisori anche n/d₁. L'elenco dei divisori non risulterà più ordinato, ma, se non abbiamo esigenze di stamparli in ordine, questo non crea problemi. Nel programma proposto abbiamo introdotto un ordinamento, appunto per comodità di stampa.

function calcola()
{
document.getElementById('risultato').value="";
var min=parseInt(document.getElementById('minimo').value);
var max=parseInt(document.getElementById('massimo').value);
if (isNaN(min) || isNaN(max)|| min<0 || max<0) //controllo dell'input
  {
  window.alert("Dati in ingresso non validi.\nInserisci interi maggiori o uguali a 0.");
  return; //L'istruzione causa l'interruzione della funzione, perchè essa non è calcolabile
  }
if ((min>10000 || max>10000) && (Math.abs(min-max)>100))
  {
  if (!window.confirm("Con i dati che hai introdotto potrei averne per ore!!\nIn ogni caso se proprio vuoi rischiare premi OK."))
  {
  return;
  }
}
if (max<min) //scambio in modo da avere max sempre più grande di min
  {
  var temp;
  temp=min;
  min=max;
  max=temp;
  }
if (min==1) min=2;
if (max==1) max=2;
var divisori=new Array(); //array dove piazziamo i divisori propri del numero in esame
divisori[0]=0;
var perfetti=0; //variabile dove piazziamo quanti perfetti abbiamo trovato
for (var k=min;k<=max;k++) //ciclo for per scandire i numeri dell'intervallo proposto dall'utente
  {
  var j=0; //variabile per indicizzare i divisori trovati
  for (var i=2;i<Math.sqrt(k);i++)
    {
    if (k%i == 0)
 {
 j++;
 divisori[j]=i; //aggiungo il divisore trovato
 j++;
 divisori[j]=Math.floor(k/i); //aggiungo anche il divisore complementare
 } //end of if
    } //end of for(var i...)
  if (k%Math.sqrt(k)==0) //se del caso si aggiunge anche la radice quadrata del numero
    {
    j++;
    divisori[j]=Math.sqrt(k);
    }
  var somma=1; //Il divisore 1 non esce dal calcolo precedente
  for (var p=1;p<=j;p++)
    {
    somma=somma+divisori[p];
} //end of for (var p...)
  if (k==somma)
    {
    perfetti++;
    document.getElementById('risultato').value=document.getElementById('risultato').value+"**Il numero "+k+" è perfetto.**\n";
    var divisori1 = new Array(); /*uso questo array per piazzare solo i divisori del numero in esame,
in modo da poterlo ordinare senza problemi con residui dei divisori
di altri numeri già esaminati*/
    divisori1[0]=1;
    for (var p=1;p<=j;p++)
 {
 divisori1[p]=divisori[p];
 }
    divisori1.sort(function(a,b) {return a-b;}); //ordinamento numerico crescente
    var output="1 "; //in questa stringa metterò i divisori, appena ordinati, separati da uno spazio
    for (var p=1;p<=j;p++)
 {
 output=output+divisori1[p]+" ";
 }
    document.getElementById('risultato').value=document.getElementById('risultato').value+"I suoi divisori sono: "+output+"\n";
    } //end of if k==somma
  } //end of for(var k...)
if (perfetti==0)
  {
  document.getElementById('risultato').value=ingresso.risultato.value+"\n Non esistono numeri perfetti nell'intervallo richiesto.";
  }
} //end of calcola()

 

Commenti:

• Il metodo sort dell'oggetto array (che dunque si richiama con nomearray.sort()) ordina, sul posto, un array. L'ordinamento avviene per default in ordine alfabetico e per produrre un ordinamento numerico occorre passare al metodo sort un "letterale funzione" come nell'esempio. Torneremo su questo quando faremo esempi di ordinamento. Per ora si può ricordare che la chiamata nomearray.sort() senza alcun parametro ordina l'array in ordine alfabetico, la chiamata nomearray.sort(function(a,b) {return a-b;}) ordina l'array in ordine numerico crescente.
• In una prima versione di questo codice avevamo scritto la seguente riga:
     for (var i=2;i<=Math.sqrt(k);i++)
  al posto di  questa:
     for (var i=2;i<Math.sqrt(k);i++).
  Nel caso dei quadrati perfetti ciò provocava un errore nel calcolo dei divisori, in quanto la radice quadrata del numero veniva contata due volte, una volta direttamente, la seconda con l'aggiunta del "divisore complementare". Un nostro allievo (Giovanni Pizzi della IVB 2001/2002) del Liceo Grigoletti ci ha segnalato il bug. Il bug è di quelli che non si riesce a trovare facilmente, perché i numeri su cui testare il programma (cioè i numeri perfetti noti e trattabili) non sono quadrati perfetti. Si tratta di un esempio interessante di come sia, a volte, estremamente difficile scrivere codici esenti da errori, anche dopo accurati test. La modifica è consistita nel limitare il ciclo for (ai valori minori e non minori od uguali alla radice quadrata del numero) e contemporaneamente nell'eseguire un test speciale per la radice quadrata del numero: if (k%Math.sqrt(k)==0)....
• Ulteriori modifiche al codice sono state poi proposte da un altro nostro allievo (Zamuner Alberto della IVB 2002/2003) del Liceo Grigoletti: il codice non funzionava in alcune particolari situazioni, a causa di un bug, anch'esso di difficile individuazione, proprio a causa della difficoltà "tecnica" di testare i risultati.

Esercizio proposto

• Costruire un programma che ricerchi solo i perfetti pari, utilizzando il teorema di Eulero (purtroppo anche con questo metodo non si fanno grandi progressi perché i numeri perfetti superano presto le capacità del computer: il più grande numero perfetto conosciuto -almeno fino al gennaio 1998- è 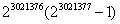, e si tratta solo del 37°!).

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 01/11/2001 - ultimo aggiornamento il 01/09/2003