Le circonferenze per due punti e tangenti ad una retta data
Sono dati due punti A e B ed una retta r e si chiede di trovare le circonferenze passanti per i due punti e tangenti alla retta. Il problema ha soluzioni solo se i due punti stanno entrambi nello stesso semipiano dei due individuati dalla retta e se almeno uno dei due è esterno alla retta.
Considereremo tre diverse costruzioni, sempre con riga e compasso, la prima usa il teorema della secante e della tangente, la seconda le proprietà dei fasci di circoli, l'ultima l'inversione circolare.
Prima costruzione
Conviene distinguere tre casi:
1 - I due punti stanno su una parallela alla retta data
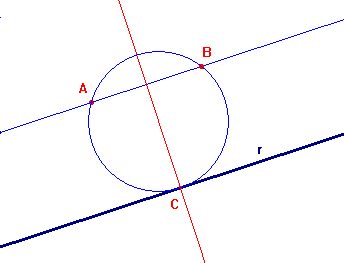
In questo caso esistono due "circonferenze" che risolvono il problema, di cui una degenere e coincidente con la retta passante per i due punti dati. Per trovare l'altra è sufficiente tracciare l'asse del segmento AB, determinare il punto C di intersezione di quest'asse con la retta r e costruire la circonferenza passante per i tre punti A, B, C, come mostrato nel primo caso dei problemi di Apollonio.
2 - I due punti non stanno su una parallela alla retta data e sono esterni alla retta
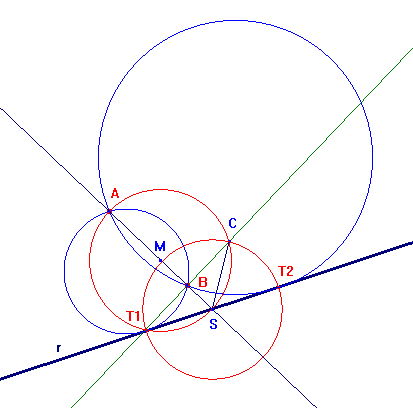
In questo caso la costruzione si fa agevolmente se si osserva che, detti T il punto di tangenza tra una delle circonferenze cercate e la retta r, ed S il punto di intersezione tra AB ed r, il segmento ST è medio proporzionale tra SB ed SA (teorema della secante e della tangente). Per costruire questo medio proporzionale si traccia la circonferenza avente centro nel punto medio, M, di SA e successivamente la perpendicolare per B ad SA. SC è il medio proporzionale cercato (primo teorema di Euclide). Riportato C su r (mediante la circonferenza di centro S e raggio SC) in T1 e T2 si tracciano, come mostrato nel primo caso dei problemi di Apollonio, le circonferenze per A, B, T1 e per A, B, T2: queste soddisfano le condizioni del problema.
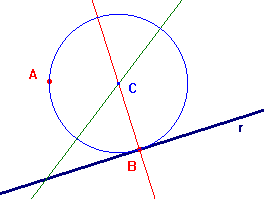
3- Uno dei due punti sta sulla retta data
La costruzione è, in questo caso, quasi immediata: il problema ha un'unica soluzione e la circonferenza cercata ha centro nel punto C di intersezione tra la perpendicolare ad r per B e l'asse del segmento AB.
Seconda costruzione
Ci occupiamo solo del caso in cui i due punti sono esterni alla retta data e appartengono allo stesso semipiano dei due individuati dalla retta. Negli altri casi la costruzione é identica a quella di sopra. Questa costruzione si basa sulle proprietà dei fasci di circoli: é chiaro che i circoli che cerchiamo appartengono al fascio avente i due punti dati come punti base.
Siano dati i due punti A e B e la retta r. Consideriamo un qualunque cerchio passante per A e B (e indichiamone con O il centro). Consideriamo poi il cerchio di centro L (intersezione tra AB e la retta data) e ortogonale al cerchio di centro O (basta condurre da L una tangente al cerchio in questione). Questo cerchio appartiene al fascio di punti limite A e B (ortogonale al fascio di punti base A e B). I punti T1 e T2 di intersezione tra quest'ultimo cerchio e la retta data completano, con A e B, due terne di punti per cui devono passare i cerchi richiesti (in quanto essi devono essere ortogonali al cerchio di centro L). L'animazione mostra che la scelta di O è ininfluente agli effetti della costruzione.
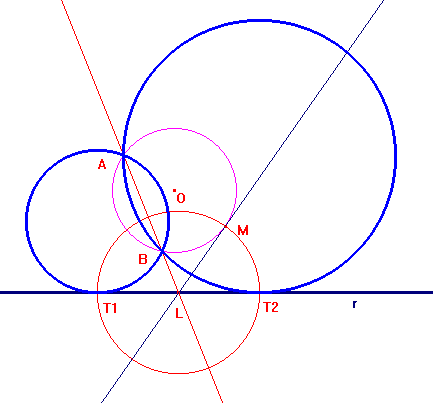
Terza costruzione
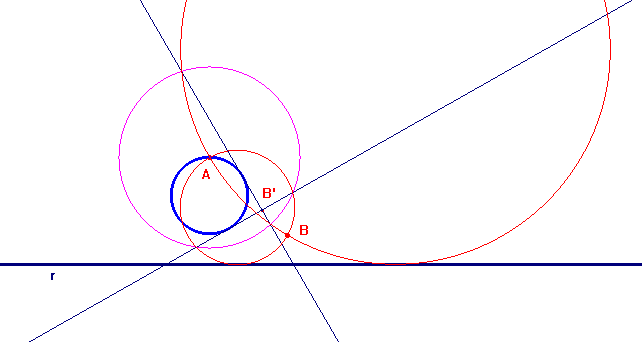
Dati i punti A e B e la retta r, si consideri un'inversione avente centro in uno dei due punti, per esempio A, e raggio qualunque (in violetto il circolo di inversione nella figura). Si consideri il circolo γ inverso della retta r (in blu nella figura) e l'inverso B' di B. Da B' si traccino le tangenti a γ. I cerchi inversi di queste due rette tangenti soddisfano i requisiti richiesti. La costruzione si semplifica un po' se si sceglie AB come raggio del circolo di inversione: in questo caso B e B' coincidono. Questa scelta è importante in una costruzione "manuale", diventa irrilevante se si usa un programma di geometria dinamica come Cabri. Si veda un'animazione della costruzione finale, con CabriJava. In questa animazione è possibile anche verificare che la scelta del raggio del circolo di inversione è ininfluente ai fini del risultato.