Curve asintotiche
Sia y=f(x) una funzione definita in un intorno di
+∞ (analoghe considerazioni per le funzioni definite in un
intorno di -∞). Se la funzione si può decomporre
nella somma f(x)=g(x)+h(x) e se 
, diremo che la y=g(x) è una curva asintotica a
f(x), per 
.
Questa definizione è giustificata dalla seguente
osservazione: presi due punti P e Q, rispettivamente sul grafico
di f(x) e di g(x), aventi la medesima
ascissa, la differenza , 
, fra le loro ordinate tende a zero al tendere di x a
+∞, in perfetta analogia con la definizione di asintoto.
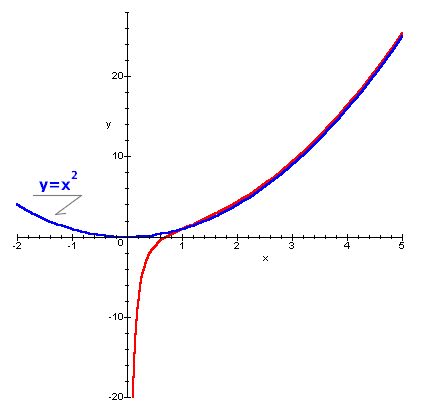
Un esempio è fornito da 
: y=x2 è una curva asintotica
a f(x), per .
Una funzione può avere anche più curve asintotiche.
Si consideri per esempio la funzione
. Poiché si può
scrivere: 
, oppure 
, oppure 
, si ottiene che
f(x) è asintotica a
, a
, a
.
Il caso più importante è quello delle funzioni razionali fratte 
, essendo N (=anxn+...) e D
(=bmxm+...) due polinomi
nell'indeterminata x. Per queste funzioni non occorre fare
distinzione tra +∞ e -∞ e si può seguire il
seguente schema semplificato per la ricerca degli asintoti
orizzontali ed obliqui:
-
Se deg(N)<deg(D), allora
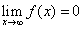, da cui segue che y=0 è asintoto
orizzontale.
-
Se deg(N)=deg(D), allora
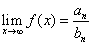, da cui 
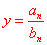è asintoto orizzontale.
-
Se deg(N)>deg(D), si esegua la divisione tra N e D, ottenendo
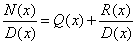, con
deg(Q)=deg(N)-deg(D) e deg(R)<deg(D). Se ne deduce che
y=Q(x) è
asintotica a f(x): se deg(Q)=1, si tratta
di un asintoto, se
deg(Q)>1 si tratta di una curva
asintotica.
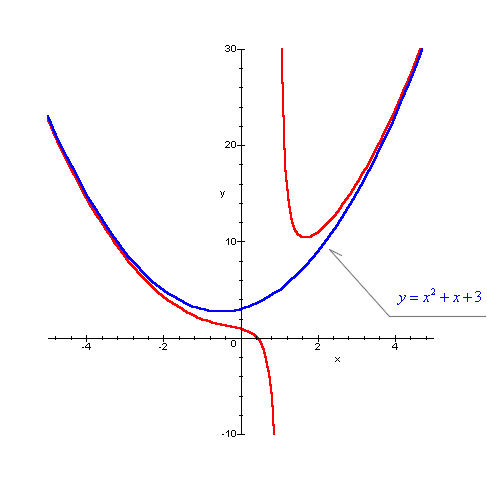
Come esempio di funzione razionale fratta con curva
asintotica si può prendere 
, che ha come parabola asintotica la
y=x2+x+3.
