Successioni e ricorsione
Come è noto si chiama successione di numeri reali una
funzione 
. Se A è finito la
successione si dice finita, altrimenti si dice
infinita. Di norma, se non ci sono ulteriori
precisazioni, per successione si intende una successione
infinita con l'insieme A coincidente con tutto N,
eventualmente privato solo di qualcuno dei suoi primi
elementi.
Per queste particolari funzioni si usano notazioni speciali: di
solito si usano le lettere a, b
anziché f, g; inoltre la
variabile, che si indica con n, non si mette tra
parentesi, ma come pedice accanto al nome della funzione (si
scrive cioè 
anziché 
). I valori an si chiamano
anche termini della successione ed
an stesso è detto termine
n-esimo. Spesso per indicare una successione si elencano,
in ordine, gli elementi del codominio; si usa dire, per esempio:
sia data la successione a1 , a2 ,
a3 , ... ,an, .... In molti casi si
usa anche la notazione {an} per indicare una
successione.
Le successioni, oltreché come detto (cioè in maniera "esplicita"), si possono anche definire per ricorsione, sulla base del principio di induzione. Un oggetto è detto ricorsivo se è definito, almeno parzialmente, in termini di se stesso.
Consideriamo per esempio la potenza di un numero reale k, con esponente intero n: essa si può definire in due modi, perfettamente equivalenti.
-
Mediante la definizione "esplicita"
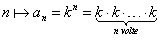, considerando a parte il caso
k0 e k1.
-
Per ricorsione, ponendo:
.
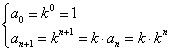La seconda definizione si può "leggere" in due modi. Supponiamo per esempio di voler calcolare 34, allora:
- Partendo da 0 si ottiene 30=1, 31=3.30=3, 32=3.31=3.3=9, 33=3.32=3.9=27, 34=3.33=3.27=81.
- Partendo da 4 si ottiene: 34=3.33, e poiché non conosco 33, sospendo un momento il calcolo e cerco di trovarlo; dalla stessa formula trovo che 33=3.32: ragionando nello stesso modo vado a calcolare 32; 32=3.31; e ancora: 31=3.30; ma ora so che 30=1 e quindi, procedendo a ritroso, trovo 31=3, 32=9, 33=27, 34=81. Si noti l'importanza del valore iniziale: non solo cambiando questo valore cambia tutta la successione (come è ovvio), ma soprattutto se non avessi fissato un punto di partenza il procedimento indicato non avrebbe potuto mai avere termine!.
Dal punto di vista pratico non ci sono sostanziali differenze nei due modi di procedere. Esaminiamo invece che cosa succede dal punto di vista della implementazione in un linguaggio informatico (con particolare riguardo a Javascript, anche se la sostanza rimane identica in qualunque linguaggio di programmazione).
-
Nel primo caso dovremo introdurre una variabile (diciamo
k) dove piazzare il valore di k
(nel nostro caso 3), una (diciamo n) dove
piazzare il valore di n (nel nostro caso 4) e una
(diciamo pot, che inizializziamo ad 1) dove
piazzare il valore della potenza. Dovremo poi costruire, per
esempio con una function, un algoritmo di
calcolo che contenga un ciclo iterativo. Potrebbe essere
grossomodo così:
function potenza()
{
if (n = = 0) pot = 1
else for (i =1; i <= n; i++) pot = k*pot;
return pot;
}
Se dovessimo calcolare 3100, basterebbe solo cambiare il valore di n, ma nulla cambierebbe nell'algoritmo né, ed è quello che qui ci interessa, nella occupazione di memoria del computer. -
Nel secondo caso dovremmo introdurre le stesse variabili e
ancora una function, che però
dovrebbe continuamente richiamare se stessa. Potrebbe essere
grossomodo così:
Nel punto del programma dove la function potenza viene richiamata, le vengono passati due valori, k ed n. La function dovrebbe essere di questo tipo:
function potenza(k,n)
{
if (n = = 0) pot=1
else pot = k*potenza(k,n-1)
return pot;
}
Anche qui non c'è sostanziale differenza se invece di 34 devo calcolare 3100, ma bisogna tenere conto che ad ogni passo viene richiamata la stessa funzione potenza mentre il calcolo in corso di esecuzione "rimane sospeso", occupando di conseguenza una certa quantità di memoria: in certi casi complessi si possono anche avere problemi di overflow. Per questo alcuni linguaggi di programmazione impediscono (forse impedivano, perché oggi non succede più) l'uso della chiamata ricorsiva di una funzione (esempio il FORTRAN).
Il primo dei due metodi di procedere viene chiamato algoritmo iterativo, mentre si riserva il nome di algoritmo ricorsivo vero e proprio al secondo.
Riassumendo quanto fin qui osservato possiamo concludere che la definizione per ricorsione può essere vista nel seguente modo: si deve assegnare un punto di partenza e poi una legge che mi permetta di ricavare un termine della successione in funzione del precedente. In termini formali:
Una successione è definita per ricorrenza se è dato un valore iniziale (a0) e una funzione f(x) tale che an+1=f(an). Il valore a0 è chiamato anche seme, mentre la successione ottenuta si chiama orbita del seme relativa alla funzione f.
Nel caso della potenza la funzione f(x) è la funzione f(x)=k.x mentre a0=1.
E' chiaro che un procedimento del genere è lecito se f(an) appartiene al dominio di f per ogni n. La cosa è sicuramente vera per le funzioni in cui l'immagine coincide con il dominio e, normalmente, ci limiteremo a queste.
Ci sono altre situazioni di grande interesse che utilizzano sostanzialmente lo stesso principio della ricorsione appena introdotto per definire successioni, con una leggere modifica. Per focalizzare il problema consideriamo qualche esempio.
Il fattoriale di un numero
La definizione più semplice è la seguente: 
. In questo caso il valore di
an+1 dipende non solo dal valore di
an, ma anche da quello di n: in
sostanza dobbiamo avere un punto di partenza (come sopra) ed una
funzione f(x,n) in modo che
an+1=f(an,n). La funzione
f è data da f(x,n)=(n+1)x.
La successione dei quadrati dei numeri naturali
Oltre alla definizione canonica "esplicita" (
) si può anche dare la seguente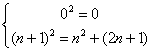 
, ricavata per semplice applicazione della formula
del quadrato di un binomio. Questa definizione mette in luce una
interessante proprietà della successione dei quadrati
perfetti (la differenza tra un quadrato perfetto e il precedente
dà la successione dei dispari) ed è dello stesso
tipo di quella data per i fattoriali, con
f(x,n)=x+(2n+1).
La successione dei cubi dei numeri naturali
Ripetendo il ragionamento appena fatto per i quadrati si
può scrivere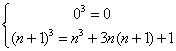 
. Questa formula
mostra ancora che il valore di an+1 dipende
da an e da n: si ha
f(x,n)=x+3n(n+1)+1.
La successione di Fibonacci
Consideriamo ora la successione definita da: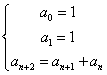 
. In questo caso ogni termine della successione è
definito come funzione dei due precedenti:
an+2=f(an+1,an). La
funzione f è ora funzione di due variabili
x1 e x2 ed è data
da:
f(x1,x2)=x1+x2.
Si tratta della famosissima successione di Fibonacci: 1, 1, 2,
3, 5, 8, 13, ...
In generale una successione definita per ricorrenza o ricorsione è definita da una funzione f(n,x1,x2,...xk), che fornisce an+k in funzione di n e dei precedenti k termini. Sarà necessario assegnare anche i valori "iniziali" dei primi k termini.