Introduzione informale, quasi per scherzo
Il problema che ci spinge a introdurre un nuovo insieme di numeri è, dunque, quello della risoluzione di certe equazioni. Cominciamo dalla più semplice: x2+1=0. Ci si accorge immediatamente che l'impossibilità di risolvere questa equazione è legata al fatto che non si può estrarre la radice quadrata di -1: non esiste alcun numero reale il cui quadrato sia -1.
Se il problema è questo, prendiamo il toro per le corna e "inventiamoci", anzi "immaginiamoci", un nuovo oggetto che indichiamo con i, e chiamiamo unità immaginaria, con la proprietà che il suo quadrato sia il numero reale -1. Poniamo cioè, per definizione,
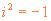
E' chiaro che la cosa, detta in questi termini, ha poco (o nessun) senso. Per intanto però andiamo avanti ugualmente cercando di fare tutte le operazioni che siamo abituati a fare con i reali, trattando questo nuovo oggetto come se fosse una lettera in un'espressione algebrica, con in più la caratteristica speciale che il suo quadrato vale -1. Naturalmente vogliamo che anche tutte le solite proprietà delle operazioni siano verificate.
Poiché in questa pagina vogliamo procedere in modo assolutamente informale, proviamo a fare subito alcuni calcoli, via via più complessi e vediamo che cosa succede. Dobbiamo procedere come nel calcolo letterale, solo aggiungendo la nuova "regola" che abbiamo introdotto ad hoc.
i3 =
i2·i =
(-1)·i = -i.
i4 =
i2·i2 =
(-1)·(-1) = 1.
(1+i)·(1-i) =
1-i2 = 1-(-1) = 2.
(1-2i)·(3+i) =
3+i-6i-2i2 =
3+i-6i-2·(-1) = 5-5i.
(2+i)3 =
8+12i+6i2+i3 =
8+12i+6·(-1)+(-i) = 2+11i.
Come si vede in particolare dagli ultimi due esempi,
semplificando opportunamente le espressioni date si riesce
sempre a scrivere il risultato nella forma
a+bi, dove a e b sono numeri
reali. Chissà se la cosa è possibile anche
eseguendo divisioni. Si tratta solo di provare. L'unico
aiuto extra che forniamo al lettore è quello di applicare
una tecnica simile a quella che abbiamo usato per
"razionalizzare" il denominatore di una frazione dove
compariva la somma di due radicali quadratici: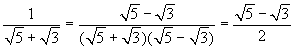 
. Nel caso della
razionalizzazione in sostanza abbiamo operato in modo da
"far sparire" le radici al denominatore, qui opereremo
in modo da "far sparire" la i al
denominatore.
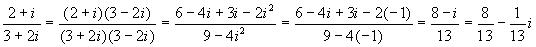
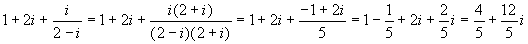
Dunque eseguendo addizioni, moltiplicazioni, divisioni, in maniera puramente formale, tra questi nuovi oggetti si ottengono sempre oggetti dello stesso tipo. Ma torniamo un momentino indietro: eravamo partiti con l'idea di risolvere equazioni e ci eravamo accorti che, almeno nel caso semplice considerato (x2+1=0), le difficoltà incontrate erano legate all'impossibilità di calcolare le radici dei numeri negativi. Nel caso di -1 il problema l'abbiamo risolto con uno stratagemma; nel caso degli altri negativi, che cosa succede? Lasciamoci guidare dalla stessa idea di prima: quello che chiediamo è che, a parte il fatto nuovo che i2 deve fare -1, tutto il resto deve rimanere invariato. Allora per calcolare la radice, per esempio, di -5 potremo procedere così:
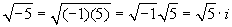
Eccezionale: funziona proprio tutto! Attenzione però:
qui, come già nei reali, ci sono due numeri che elevati
al quadrato fanno 5, uno è quello scritto sopra,
l'altro è il suo opposto, cioè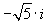 
, ma questo è un altro
problema, su cui torneremo più avanti in maniera
dettagliata. E' proprio tutto a posto, almeno per quanto
riguarda il calcolo delle radici quadrate? In realtà un
piccolo sospetto ci dovrebbe venire: abbiamo introdotto una
entità misteriosa per poter calcolare le radici dei
numeri negativi, questo ci ha condotto a lavorare con
oggetti di un nuovo tipo (che si scrivono nella forma
a+bi), ma ora possiamo calcolare le radici di
questi nuovi oggetti? Se la risposta fosse negativa dovremmo
chiaramente abbandonare l'idea che ci è venuta. Non
ci resta quindi che provare, procedendo secondo lo schema
già utilizzato sopra.
Consideriamo il numero 1+i e
poniamoci la seguente domanda: esistono cose del tipo
x+iy (con valori di x e y opportuni)
tali che (x+iy)2=1+i? Se oggetti di
questo tipo ci sono, bisogna che
x2+2ixy-y2=1+
i. Possiamo ora invocare il "principio di
identità dei polinomi" per concludere che deve
essere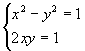 
(uguaglianza dei "termini
noti" e dei "coefficienti di i").
Risolvendo il sistema si trovano due soluzioni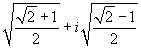 
e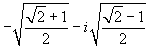 
.
A questo punto cominciamo ad essere soddisfatti: riusciamo a calcolare le radici quadrate non solo dei vecchi numeri negativi, ma anche di questi nuovi oggetti misteriosi (che cominciano a diventare sempre meno misteriosi!). Ma siccome siamo curiosi facciamo un'altra prova.
Consideriamo di nuovo il numero -1 (il punto
di partenza delle nostre indagini) e poniamoci la seguente
domanda: esistono cose del tipo x+iy (con valori di
x e y opportuni), tali che
(x+iy)3=-1. Naturalmente una di queste cose
c'è sicuramente, ed è il numero -1 stesso (che
corrisponde ad x=-1 e y=0), ma nessuno ci
vieta di provare a vedere se ce ne sono anche altre. Si
può impostare un sistema come nell'esempio di prima e
si trovano le seguenti due nuove soluzioni: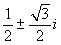 
.
Il tutto si fa veramente interessante: il risultato dell'ultimo esempio equivale a dire che l'equazione x3+1=0 ha tre soluzioni distinte (cioè tante quant'è il suo grado) e questo era proprio il nostro problema di partenza! Naturalmente è presto per concludere che tutto funziona, ma perlomeno siamo sulla strada giusta: l'idea di introdurre un nuovo oggetto con la strana e inusuale proprietà che il suo quadrato sia -1, comincia a piacerci proprio.
Da buoni matematici non possiamo però procedere oltre senza dare una giustificazione formalmente corretta a quanto abbiamo finora detto, ma, come vedremo, dopo questa "chiacchierata" non ci saranno grossi problemi tecnici (almeno all'inizio!).
Per intanto riassumiamo il contenuto di questa pagina: per costruire un nuovo insieme di numeri in cui sia possibile fare sempre le radici quadrate, abbiamo introdotto un nuovo simbolo, i, con la proprietà che il suo quadrato valga -1, e, di conseguenza, abbiamo imparato ad operare con oggetti del tipo a+ib, dove a e b sono numeri reali. In sostanza l'idea che abbiamo avuto ci ha portato ad operare con un oggetto misterioso, i, e con coppie di numeri reali. E' proprio partendo dalla considerazione di queste coppie che introdurremo in modo formalmente corretto i nuovi numeri. L'idea di utilizzare coppie di oggetti già noti l'avevamo già sfruttata sia per costruire i numeri interi sia, soprattutto per costruire i numeri razionali, partendo da "frazioni" con un numeratore e un denominatore. Per i dettagli puoi consultare nella monografia sull' estensione del concetto di numero.