La sezione aurea
La sezione aurea di un segmento interviene in numerose questioni di geometria e in molte applicazioni, per esempio nell'architettura. Si tratta, dato un segmento AB, di dividerlo in due parti AH e HB in modo che la prima sia media proporzionale tra l'intero segmento e la parte restante.
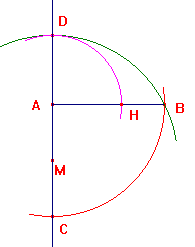
La prima costruzione di Euclide si trova molto presto, nel Libro II , Proposizione 11, ed è riportata qui sopra. Con centro in A e apertura AB si individua il punto C sulla perpendicolare ad AB per A. Con centro nel punto medio M di AC e apertura MB si trova il punto D. Con centro in A e apertura AD si trova H: AH è la sezione aurea richiesta.
In termini algebrici moderni la prova è immediata: si deve solo verificare che, se a è la lunghezza di AB, AH è la soluzione positiva dell'equazione a(a-x)=x2.