Costruzione di un triangolo dati ha, ma, R
La costruzione è abbastanza semplice. Supposto risolto il problema si vede subito che il triangolo AHaMa è facilmente costruibile e che si può tracciare l'asse del lato BC, su cui si trova il circocentro.
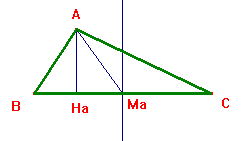
Siano allora dati tre segmenti che individuano rispettivamente l'altezza e la mediana relativa al lato a e il raggio del cerchio circoscritto.
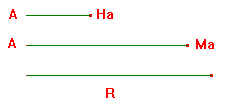
A partire da un punto A costruiamo il triangolo rettangolo di cateto AHa e ipotenusa AMa. Per Ma tiriamo la perpendicolare, che sarà l'asse del lato BC, e con centro in A tracciamo una circonferenza di raggio R. Le sue due intersezioni O' e O'' (se esistono) con l'asse appena costruita saranno i possibili circocentri del costruendo triangolo. I vertici B e C saranno le (eventuali) intersezioni delle circonferenze di centri O' e O'' con la retta HaMa. Ci possono essere uno o due triangoli che soddisfano i requisiti.
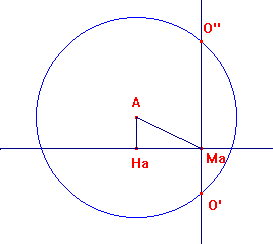
La Cabri costruzione non richiede alcuna particolare attenzione. Muovendo i punto Ha ed Ma, o l'estremo del segmento R puoi variare i dati del problema.