Osservazioni su cerchi inscritti ed ex-inscritti
I punti di contatto tra un triangolo e i suoi cerchi inscritto ed ex-inscritti sono in relazioni interessanti tra di loro e con i vertici del triangolo stesso. Queste relazioni sono molto utili nella costruzione di triangoli e le riassumiamo brevemente qui.
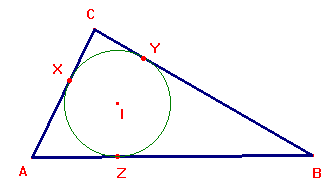
Dato un triangolo ABC e il suo cerchio inscritto, si ha CX=CY, AX=AZ, BY=BZ. Sommando questi sei segmenti si ottiene il perimetro 2p. Se ne deduce facilmente che la distanza di ogni vertice dal punto di contatto con l'incerchio è il semiperimetro meno il lato opposto:
CX = CY = p-c ; AX = AZ = p-a ; BY = BZ = p-b
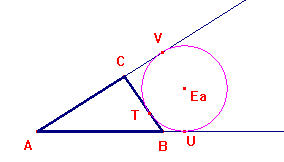
Consideriamo ora uno degli ex-cerchi e i suoi punti di contatto con un lato e i prolungamenti degli altri due. Essendo CV=CT e BU=BT se ne deduce subito che AV = AU = p. Per differenza si deduce anche facilmente che BU = BT = p-c.
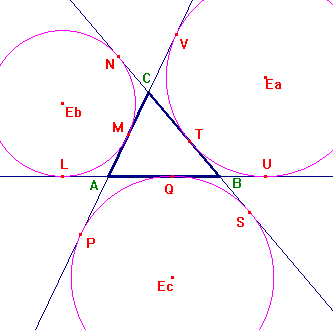
Considerando i tre ex-cerchi si può dedurre ancora che BL=AU=p, da cui
- BU = AL = BT = AM = p-c
- BS = CN = BQ = CN = p-a
- AP = CV = AQ = CT = p-b
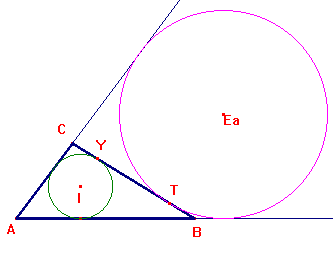
Consideriamo infine l'incerchio e uno degli ex-cerchi. Essendo CY = BT = p-c, si ottiene facilmente YT = a - 2(p-c) = c-b.
Ovvero: la distanza tra i punti di contatto dell'incerchio e di un ex-cerchio, su un lato di un triangolo, è la differenza tra gli altri due lati del triangolo.