Le tangenti comuni a due circoli dati
Tra le numerose costruzioni possibili segnaliamo quella che utilizza la cosiddetta dilatazione parallela, utile soprattutto quando si debbano trattare rette e cerchi tra loro tangenti: si immagina che il raggio di uno dei cerchi in questione tenda a zero, mentre le rette e i restanti cerchi seguono questo movimento rimanendo tangenti e mantenendo il centro (i cerchi) o la direzione (le rette). La costruzione che faremo renderà chiaro il metodo.
Siano allora dati due cerchi Q e P, di raggi rispettivamente R ed r.
Supposto risolto il problema, consideriamo una delle due tangenti "esterne", t, e immaginiamo di far tendere a zero il raggio del cerchio più piccolo. La tangente si porterà nella posizione t' e sarà tangente al cerchio di raggio R-r.
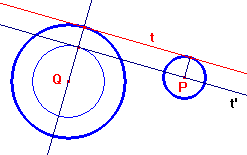
Consideriamo poi una delle due tangenti "interne", s. Nelle stesse condizioni di prima essa tenderà alla posizione s' e sarà tangente al cerchio di raggio R+r.
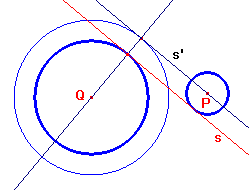
Per risolvere il problema basterà allora condurre dal centro della circonferenza più piccola le tangenti alle circonferenze che hanno centro sul centro della circonferenza più grande e raggi rispettivamente R+r e R-r.
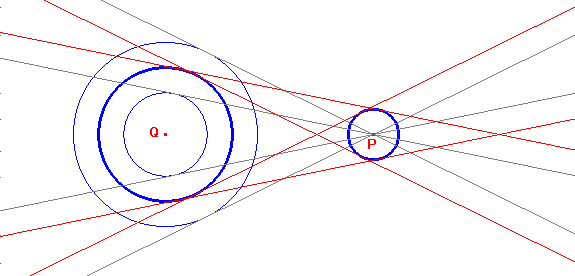
La Cabri costruzione richiede la preventiva determinazione di quale delle due circonferenze ha raggio minore: cambiando dinamicamente i raggi dei cerchi, i ruoli delle circonferenze si possono invertire e la costruzione può non essere più valida.
Nella figura qui sotto, muovendo i punti Q e P puoi spostare i centri delle circonferenze, tirando le circonferenze puoi far variare i loro raggi. Solo la situazione di tangenza (interna od esterna) tra le due circonferenze non è gestita dinamicamente in modo ottimale.