Costruzione di un triangolo date le mediane
La costruzione si può fare con metodi elementari. L'uso di Cabri, anche per la ricerca del tipo di costruzione, è molto utile.
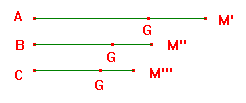
Siano allora date le tre mediane; su ciascuna di esse individuiamo la posizione del baricentro, G, con la solita divisione di un segmento in tre parti. M', M'', M''', sono i punti medi dei lati opposti.
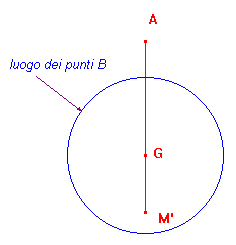
Costruiamo ora, a partire da un punto A qualunque, un segmento AM' uguale alla prima delle tre mediane date e individuiamo su di esso il punto G. Il punto B apparterrà alla circonferenza, che si costruisce facilmente, di centro G e raggio BG.
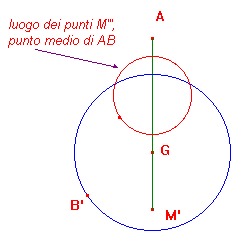
Se su questa circonferenza prendiamo un punto qualunque (che indichiamo con B'), possiamo individuare la posizione del generico punto M''' come punto medio del segmento AB'. Al variare di B' sulla circonferenza possiamo ottenere il luogo descritto dal punto medio citato. Cabri costruisce facilmente questo luogo che sembra essere una circonferenza.
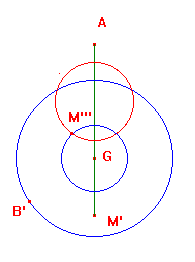
Possiamo ora osservare che il punto M''' deve stare anche sulla circonferenza di centro G e raggio GM'''. La sua posizione è dunque individuata come intersezione tra due luoghi (ci sono due soluzioni possibili, per la simmetria del problema, e ne abbiamo indicata una).
A questo punto il gioco è fatto: B è il simmetrico di A rispetto ad M''' e C è il simmetrico di B rispetto ad M': il triangolo è costruito.
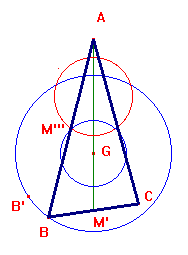
Per la Cabri costruzione ci resta da osservare che l'intersezione tra la circonferenza luogo (in rosso nelle figure sopra) e la circonferenza di centro G e raggio GM''' non è possibile in Cabri II, mentre è possibile in Cabri II plus. Possiamo dimostrare (analiticamente o sinteticamente) che il luogo è proprio una circonferenza, con centro ovviamente sulla retta AM' e raggio facilmente determinabile. La possiamo dunque, anche in Cabri II, costruire come circonferenza per trovare le intersezioni richieste. La figura qui sotto mostra il risultato finale e, muovendo i punti M', M'', M''', puoi verificare come varia il triangolo (e anche fino a che punto è costruibile!).