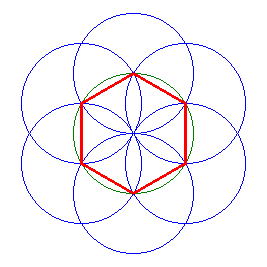
Il triangolo equilatero e l'esagono regolare
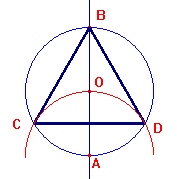
La costruzione è estremamente semplice: tracciato un diametro AB, con centro in A e apertura AO si traccia l'arco COD. Il triangolo richiesto è il triangolo CBD.
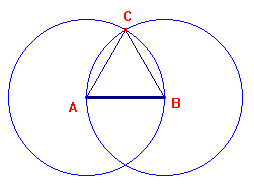
Euclide, nel libro I, Proposizione 1, si preoccupa di costruire il triangolo equilatero su un dato segmento. La costruzione, a partire dal lato assegnato AB, è indicata qui sotto, e non richiede commenti.
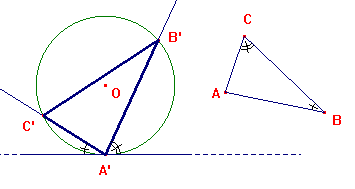
Successivamente, nel libro IV, Proposizione 2, inscrive in un cerchio un triangolo avente gli stessi angoli di uno dato. La costruzione procede come segue: dato un triangolo ABC e una circonferenza di centro O, si conduca per il suo punto A', la tangente. Basta costruire due angoli di vertice A, come in figura, uguali agli angoli ACB e ABC. Il triangolo A'B'C' è equiangolo con quello dato.
Costruito il triangolo, l'esagono segue immediatamente per bisezione. La cosa interessante comunque, provata da Euclide nel Libro IV, Proposizione 15, è che il lato dell'esagono regolare è uguale al raggio.