L'enunciato del principio
I numeri naturali giocano un ruolo molto speciale nella matematica, tanto da far dire a Leopold Kronecker (1823-1891) che "Dio creò i numeri naturali, tutto il resto è opera dell'uomo". Tra le ragioni di questa particolarità c'è, innanzitutto, la constatazione che questi numeri possono essere descritti in modo compatto come se fossero generati tutti da uno stesso oggetto: il numero "0" (o il numero "1" secondo altre convenzioni). L'idea, che non vogliamo formalizzare ulteriormente, è che ogni numero è in grado di generare un suo "successore" e che, iterando il processo non si ottiene mai un numero già considerato.
Possiamo visualizzare questo fatto con l'immagine di una successione di pezzi di domino, posti verticalmente in equilibrio ad una distanza minore della loro altezza. Facendo cadere il primo della fila, tutti gli altri cadranno in conseguenza.
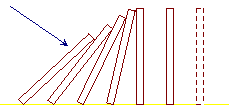
In termini insiemistici si può formalizzare questa proprietà dei naturali con la seguente affermazione: Se un insieme X contiene il numero 0 e il successivo di ogni suo elemento, allora X è un soprainsieme di N.
Da qui si ricava il principio o assioma di induzione:
![]() Se P(n) è una
proposizione dipendente da n e si sa che:
Se P(n) è una
proposizione dipendente da n e si sa che:
- P(0) è vera;
- l'essere vera P(n) implica la validità di P(n+1);
allora P(n) è vera per ogni n naturale.
Se invece si sa che
- P(m) è vera (m è un naturale qualunque);
- l'essere vera P(n) implica la validità di P(n+1);
allora P(n) è vera per ogni n naturale maggiore od uguale a m.
In termini dei pezzi di domino, questa variante equivale a far cadere non il primo pezzo, ma uno successivo.
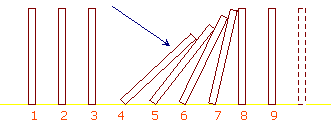
Da questo principio si ricava il seguente
Metodo di dimostrazione per induzione: Sia P(n) una affermazione dipendente da un naturale n. Se si riescono a completare i due passi seguenti:
- per un certo valore m, dimostrare che P(m) è vera;
- considerato un valore k ≥ m arbitrario ma fissato, e supposta vera P(k) dimostrare che P(k+1) è vera;
allora P(n) è vera per ogni n naturale maggiore od uguale a m.
Il primo si chiama Passo base, il secondo Passo induttivo.
Esempio 1
Provare che, per ogni naturale n > 0, ![]() .
**
.
**
Si tratta, probabilmente, della più famosa formula che si dimostra per induzione. Si noti che la prova può essere condotta in termini elementari, con il metodo proposto da Gauss in giovanissima età.
- Passo base. Se n = 1 la formula fornisce 1 = 1 che è banalmente vera.
-
Passo induttivo. Fissiamo k > 1 e
supponiamo vero che
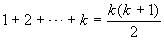 , cioè
P(k). Si ha allora:
, cioè
P(k). Si ha allora: 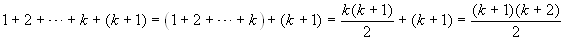 . Dunque vale P(k+1).
. Dunque vale P(k+1).
Questo permette di concludere che la proprietà è vera per ogni n>1.
Si noti che non abbiamo affermato che P(k) sia vera, ma solamente che se P(k) è vera allora è vera anche P(k+1). Questa sola dimostrazione non permette di concludere alcunché sulla validità o meno di P(k). Si veda il successivo esempio per chiarire il concetto.
Esempio 2
Sia P(n) l'affermazione: ![]() .
Provare che se P(k) è vera per un fissato valore
k, anche P(k+1) è vera; provare che
P(n) è falsa per ogni n e dimostrare
che, invece, vale l'affermazione Q(n):
.
Provare che se P(k) è vera per un fissato valore
k, anche P(k+1) è vera; provare che
P(n) è falsa per ogni n e dimostrare
che, invece, vale l'affermazione Q(n): ![]() .
.
Fissiamo k > 1 e supponiamo vera P(k).
Consideriamo ora la situazione che si presenta per k+1;
si ottiene: ![]() . Dunque vale
P(k+1). Si controlla però facilmente che la
proprietà non è vera per n=1 (infatti 1
< 9/8).
. Dunque vale
P(k+1). Si controlla però facilmente che la
proprietà non è vera per n=1 (infatti 1
< 9/8).
Questa conclusione prova comunque che vale Q(1).
Dimostriamo ora che se è vera Q(k) è vera
anche Q(k+1). Si ha: ![]() .
Si può così concludere che Q(n) è
vera per ogni n: questa basta per provare che
P(n) è falsa per ogni n.
.
Si può così concludere che Q(n) è
vera per ogni n: questa basta per provare che
P(n) è falsa per ogni n.
![]() Dunque nella dimostrazione per
induzione entrambi i passi indicati sono essenziali!!
Dunque nella dimostrazione per
induzione entrambi i passi indicati sono essenziali!!
Di solito, negli esercizi, si indica con n anziché con k il generico, ma fissato, valore utilizzato nel passo induttivo.