I principali risultati sulle serie numeriche
Useremo le seguenti notazioni e nomenclatura per le serie:
-
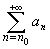 , quando sia necessario precisare il
valore iniziale dell'indice. an
è detto termine generale.
, quando sia necessario precisare il
valore iniziale dell'indice. an
è detto termine generale.
-
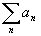 , quando il valore iniziale
dell'indice non è importante, per esempio nella
ricerca del carattere.
, quando il valore iniziale
dell'indice non è importante, per esempio nella
ricerca del carattere.
-
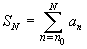 , per indicare la ridotta
N-esima.
, per indicare la ridotta
N-esima.
-
Coda di una serie è una serie del tipo
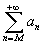 , per un opportuno valore di M.
, per un opportuno valore di M.
Condizione necessaria di convergenza.
Una serie non può convergere se il suo termine generale non è infinitesimo.
Teorema dell'aut-aut per le serie a termini di segno costante.
Una serie a termini di segno costante può solo convergere o divergere. Questo implica che una serie a termini positivi converge se e solo la successione delle sue ridotte è maggiorata. Analogo discorso per le serie a termini negativi dove la successione delle ridotte deve essere minorata.
La somma (o l'incastro) di due serie e il prodotto per una costante.
- La somma di due serie convergenti ad a e b converge ad a+b. Analogo risultato per un qualunque incastro tra le due serie.
- La somma di due serie divergenti a +∞ (a -∞) diverge a +∞ (a -∞). Analogo risultato per un qualunque incastro tra le due serie.
- La somma di una serie convergente e di una serie divergente a +∞ (a -∞) diverge a +∞ (a -∞). Analogo risultato per un qualunque incastro tra le due serie.
- Il prodotto tra una serie convergente ad a e una costante c è una serie convergente a ca.
- Il prodotto tra una serie divergente e una costante non nulla è una serie divergente.
Assoluta convergenza.
Se la serie ottenuta prendendo i valori assoluti di tutti i
termini converge, anche la serie data converge e si ha: ![]() .
.
Criterio del confronto.
Si tratta del criterio fondamentale per le serie, da cui sostanzialmente derivano tutti gli altri.
Date due serie a termini positivi ![]() e
e ![]() , tali che
, tali che ![]() ,
, ![]() n, allora:
n, allora:
-
Se
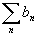 converge, anche
converge, anche 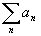 converge (Ogni minorante, a
termini positivi, di una serie convergente converge).
converge (Ogni minorante, a
termini positivi, di una serie convergente converge).
-
Se
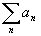 diverge, anche
diverge, anche 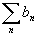 diverge (Ogni maggiorante, a
termini positivi, di una serie divergente diverge).
diverge (Ogni maggiorante, a
termini positivi, di una serie divergente diverge).
Criterio della radice (o di Cauchy).
Data una serie a termini positivi se, ![]() n,
n, ![]() , la serie
converge; se
, la serie
converge; se ![]() , la serie diverge. In
particolare se
, la serie diverge. In
particolare se ![]() , la serie
converge; se
, la serie
converge; se ![]() la serie diverge; se
la serie diverge; se
![]() nulla si può dire, a meno
che
nulla si può dire, a meno
che ![]() , nel qual caso la serie
diverge.
, nel qual caso la serie
diverge.
Criterio del rapporto o di d'Alembert.
Data una serie a termini strettamente positivi se, ![]() n,
n, ![]() , la serie converge; se
, la serie converge; se ![]() la serie diverge. In particolare se
la serie diverge. In particolare se ![]() la serie converge, se
la serie converge, se ![]() ;
; ![]() nulla si può
dire, ameno che
nulla si può
dire, ameno che ![]() , nel qual caso la
serie diverge.
, nel qual caso la
serie diverge.
Osservazioni sul criterio del rapporto e della radice
Si prova che se ![]() anche
anche ![]() (anche nel caso di limite infinito), mentre
non è vero il viceversa (si veda l'esercizio 1.17). Questo
significa che il criterio della radice è più
"generale" di quello del rapporto, anche se,
naturalmente, in alcuni casi può essere tecnicamente
più semplice l'applicazione di uno invece che
l'altro.
(anche nel caso di limite infinito), mentre
non è vero il viceversa (si veda l'esercizio 1.17). Questo
significa che il criterio della radice è più
"generale" di quello del rapporto, anche se,
naturalmente, in alcuni casi può essere tecnicamente
più semplice l'applicazione di uno invece che
l'altro.
È altresì importante osservare che i criteri della radice o del rapporto funzionano solo per serie il cui termine generale è infinitesimo di ordine soprareale, per cui è perfettamente inutile usarli quando si sa a priori che la serie non è di questo tipo.
Criterio di condensazione di Cauchy.
La serie a termini positivi ![]() , decrescente e infinitesima, converge se e solo se
converge la serie
, decrescente e infinitesima, converge se e solo se
converge la serie ![]() .
.
Criterio dell'ordine di infinitesimo.
Se una serie a termini positivi è infinitesima di ordine superiore ad un reale s > 1, essa è convergente, se invece è infinitesima di ordine ≤ 1, allora diverge.
Criterio di Leibniz.
Una serie a segno alterno, infinitesima, e tale che la successione dei valori assoluti dei suoi termini sia decrescente converge.
Criterio dell'integrale.
Se ![]() è una funzione positiva non crescente,
la serie
è una funzione positiva non crescente,
la serie ![]() e l'integrale
e l'integrale ![]() sono della stessa natura.
sono della stessa natura.
Criterio del rapporto migliorato.
Date due serie a termini positivi ![]() e
e ![]() , se, da un certo
n in poi,
, se, da un certo
n in poi, ![]() , allora la
convergenza di
, allora la
convergenza di ![]() implica la
convergenza di
implica la
convergenza di ![]() , mentre la
divergenza di
, mentre la
divergenza di ![]() implica la divergenza
di
implica la divergenza
di ![]() .
.
Criterio di Raabe (o di Raabe-Duhamel).
Data una serie a termini positivi se, da un certo n
in poi, 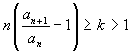 , la serie converge; se
invece
, la serie converge; se
invece 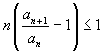 la serie diverge. In
particolare se
la serie diverge. In
particolare se 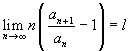 , la serie
converge quando l > 1, diverge quando l
< 1; nulla si può dire se l = 1.
, la serie
converge quando l > 1, diverge quando l
< 1; nulla si può dire se l = 1.
Criterio di Dirichlet
Sia ![]() una serie tale che la
successione delle sue somme parziali è limitata da un
numero M. Sia poi {bn} una successione
positiva, decrescente ed infinitesima. Allora la serie
una serie tale che la
successione delle sue somme parziali è limitata da un
numero M. Sia poi {bn} una successione
positiva, decrescente ed infinitesima. Allora la serie ![]() converge.
converge.
Il criterio di Leibniz è un caso particolare di questo criterio.
Criterio di Abel
Sia ![]() una serie convergente e
{bn} una successione monotòna
convergente. Allora la serie
una serie convergente e
{bn} una successione monotòna
convergente. Allora la serie ![]() converge.
converge.
Serie importanti da usare per confronto
-
Serie geometrica:
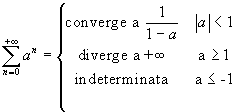 . (N.B. Se a<-1 la serie dei valori
assoluti diverge a +∞; alcuni autori chiamano
divergenti le serie di questo tipo: si tratta
più che altro di una questione di gusti).
. (N.B. Se a<-1 la serie dei valori
assoluti diverge a +∞; alcuni autori chiamano
divergenti le serie di questo tipo: si tratta
più che altro di una questione di gusti).
-
Le serie che si ottengono per derivazione da questa:
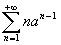 ,
, 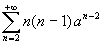 , ecc.
, ecc.
-
Serie armonica generalizzata:
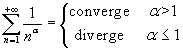 .
.
- Le serie che si ottengono per derivazione dagli sviluppi delle funzioni elementari.
Prodotto di Cauchy di due serie assolutamente convergenti
Siano ![]() e
e ![]() due serie assolutamente convergenti. La serie
due serie assolutamente convergenti. La serie ![]() ove cn =
a0bn+a1bn-1+...
+anb0, è detta prodotto
secondo Cauchy delle due serie date e converge al prodotto
delle somme delle due serie date.
ove cn =
a0bn+a1bn-1+...
+anb0, è detta prodotto
secondo Cauchy delle due serie date e converge al prodotto
delle somme delle due serie date.
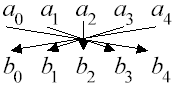
Per evidenziare graficamente il modo in cui il prodotto
è costruito, si esamini la figura seguente, in cui
abbiamo indicato i prodotti da fare per ottenere
c4: