Soluzione
Data la successione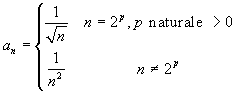 
, dimostrare che la serie
converge, trovando una maggiorazione della
successione delle ridotte.
Poiché la serie data è a termini positivi, se la
successione delle ridotte è limitata, la serie converge
(teorema dell'aut-aut). Cominciamo a considerare una ridotta
del tipo 
. Separiamo, nella ridotta, i termini
che hanno indice del tipo 2k, dagli altri. Per
semplicità poniamo 
. Allora:
.
Si ha: 
. Inoltre, poiché la serie di
termine generale 
converge, ogni sua ridotta
è minore della somma, che indichiamo con s. Si ha quindi:
. Se consideriamo ora una ridotta
Sn qualsiasi, ci sarà sicuramente una
ridotta del tipo che supera
Sn. Questo basta per concludere che la serie
data converge.
Si noti che questa serie è infinitesima, ma
non infinitesima di ordine superiore a 
.