Soluzione
Data la successione: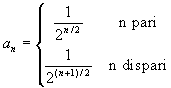 
, verificare
l'applicabilità dei criteri del rapporto e della
radice alla serie 
.
Si ha: 
. Se ne deduce intanto che il limite
di 
non esiste. Inoltre il criterio del
rapporto nella sua forma più generale non consente di
concludere, perché non vale né 
,
né 
.
Applichiamo ora il criterio della radice. Si ha: 
. Se ne deduce subito che 
.
Il criterio della radice permette di concludere che la serie
converge.
N.B. La convergenza poteva anche essere dedotta direttamente dal fatto che la serie è la somma di due serie geometriche identiche (per cui è anche facile calcolarne la somma): scopo dell'esercizio è però quello di mostrare che i due criteri, del rapporto e della radice, non sono equivalenti).