Soluzione
Studiare il carattere della serie: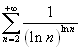 
.
Per valutare la convergenza di questa serie, costituita da termini tutti positivi, ne raggrupperemo i termini in modo da confrontarla facilmente con una serie convergente.
Cominciamo con l'osservare che tra 0 ed 1 si trova solo il
logaritmo naturale di 2 (0<ln2<1), tra 1 e 2 si
trovano i logaritmi naturali di 3, 4, 5, 6, 7
(1<ln3<ln4<ln5<ln6<ln7<2), in generale tra p e
p+1 si troveranno i logaritmi naturali di quei numeri k tali che
p<lnk<p+1, ovvero ep<k<ep+1.
Di numeri k siffatti ce ne sono al massimo
[ep+1-ep+1] (con le parentesi quadre
indichiamo la parte intera). Per ciascuno di essi si ha 
e, a maggior ragione considerato che la
disuguaglianza appena scritta è tra numeri positivi
minori di 1, 
. Se allora raggruppiamo
gli addendi della serie data mettendo assieme tutti quelli il
cui logaritmo naturale è tra p e p+1, otterremo una nuova
serie che è una minorante della serie di termine generale
, a sua volta minorante di 
. Quest'ultima serie converge (basta applicare il
criterio della radice), per cui anche la serie data converge.