La continuità uniforme
Definizioni
Una funzione f : A (
R) → R si dice
-
continua in x
A se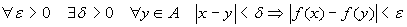 
;
-
continua in A se
;
-
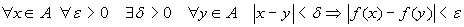uniformemente continua
in A se
;
-
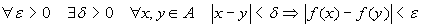Lipschitziana se esiste
una costante L>0 tale che
;
-
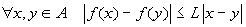α-Hölderiana
(con α>0) se esiste una costante H>0
tale che
.
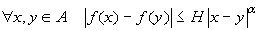Si noti, nei concetti di continuità in A e di uniforme
continuità in A, che la differenza tra le due definizioni
sta nello "spostamento" di posizione del "
x".
E' evidente che una funzione Lipschitziana è una
funzione 1-Hölderiana. Si può inoltre osservare che
se f è α-Hölderiana, con α>1
si ha: 
. La funzione ha dunque derivata nulla
e, se A è un intervallo, è costante. Si
può anche provare che se A è limitato e
f è α-Hölderiana, allora
è f è β-Hölderiana, per
ogni β≤α. Dunque ogni funzione Lipschitziana
è α-Hölderiana, per α≤1.
Osservazioni
Cerchiamo di renderci conto delle differenze tra i concetti di continuità e di continuità uniforme.
- La definizione di continuità è la richiesta che punti vicini ad un determinato punto x abbiano immagini vicine a quella di x. Ovvero: dato ε>0, si tratta di trovare δ>0, che dipenderà sia da ε che da x, in modo che punti che distano da x meno di δ abbiano immagini che distano da quella di x meno di ε.
- La definizione di continuità uniforme è invece la richiesta che punti vicini tra di loro abbiano immagini vicine tra di loro. Ovvero: dato ε>0, si tratta di trovare δ>0, che dipenderà solo ed esclusivamente da ε, in modo che coppie di punti che distano tra di loro meno di δ abbiano immagini che distano tra di loro meno di ε. Detto in altri termini si richiede che sia possibile trovare un δ>0 tale che, in un insieme di ampiezza non superiore a δ, le oscillazioni della funzione non superino ε: una funzione uniformemente continua può compiere solo "piccole oscillazioni" (in insiemi opportunamente piccoli!).
Vediamo l'interpretazione grafica dei due concetti di continuità e continuità uniforme.
Per quanto riguarda la continuità, in sostanza, fissato
un valore di ε si può trovare un valore di
δ, variabile da punto a punto, tale che il grafico della
funzione sia sempre contenuto nel rettangolo di altezza
ε e base δ, centrato in 
.
L'immagine qui sotto evidenzia che, per una funzione continua in tutti i punti del dominio, a parità di ε, il valore di δ, varia considerevolmente da punto a punto.
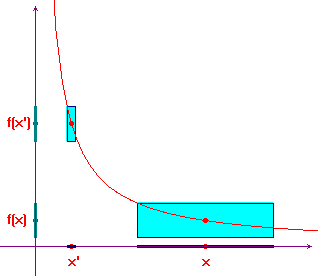
Nell'immagine dinamica qui sotto la cosa risulta ancora più evidente e si può constatare che, avvicinando il punto x all'origine, il valore di δ diventa sempre più piccolo.
La continuità uniforme si può invece interpretare nel seguente modo: fissato un valore di ε si può trovare un valore di δ tale che si possa costruire un tubicino di diametro ε e di lunghezza δ che possa essere fatto liberamente scorrere, mantenendolo sempre orizzontale, su tutto il grafico della funzione.
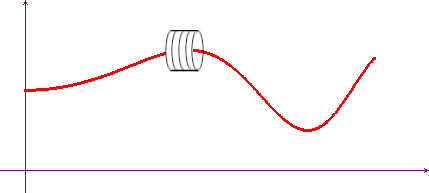
Nell'immagine dinamica qui sotto puoi sperimentare questo fatto: spostando il punto P il rettangolo giallo (che rappresenta il tubicino) può essere mosso in modo che il grafico della funzione non esca mai dalle due basi.
Risulta evidente che il concetto di continuità uniforme è molto più restrittivo che non quello di continuità: ogni funzione uniformemente continua è anche continua.
Esempi
La funzione f(x) =
x2, di R in
R, è continua in tutto il dominio.
Proviamo che essa non è uniformemente continua. Si tratta
di provare che è possibile trovare almeno due punti
"vicini" tra di loro, in modo che le loro immagini
siano invece "distanti". A tale scopo scegliamo un
valore di δ (>0) e consideriamo i due punti x
= 1/δ e y = 1/δ + δ/2. La loro
distanza è δ/2, e quindi è minore di
δ. La distanza tra le immagini è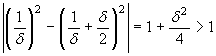 
: basterà scegliere un ε minore di 1, per
concludere che la funzione non è uniformemente continua.
Per rendersi conto a livello grafico del perché la
funzione non sia uniformemente continua basta osservare che, al
crescere di x, essa diventa molto "ripida",
nessun tubicino, per quanto corto, potrà scorrere
liberamente su tutto il grafico. Si osservi che le
difficoltà sorgono solo quando si considerano regioni del
dominio molto lontane dall'origine, e in effetti i due punti
che abbiamo considerato sopra sono tanto più grandi,
quanto più δ è piccolo.
La funzione f(x) =
x2, di I=[0,1] in R,
è continua in tutto il dominio. Proviamo che essa
é uniformemente continua. Se x ed y
sono due punti di I, si ha 
. Fissato
ε>0, basterà allora prendere
δ=ε/2 per concludere. A differenza
dell'esempio precedente questa volta la funzione è
uniformemente continua, come conseguenza del fatto che abbiamo
considerato solo una parte limitata del dominio: questo ci
assicura l'esistenza di un tubicino di lunghezza opportuna,
qualunque sia il suo diametro
Le funzioni f(x) =
sinx e g(x) = cosx, di
R in R, sono continue in tutto
il dominio. La continuità uniforme discende subito dalle
disuguaglianze |cosx-cosy| ≤
|x-y| e |sinx-siny| ≤
|x-y|: fissato ε>0, basterà
prendere δ=ε.
La funzione f(x) =
sin(x2), di R in
R, è continua in tutto il dominio.
Proviamo che essa non è uniformemente continua. A tale
scopo fissiamo un k>0 e consideriamo i punti 
. La distanza delle loro immagini vale sempre 2,
qualunque sia k. Si ha poi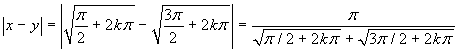 
.
Dunque la distanza tra x ed y può
essere resa arbitrariamente piccola, pur di prendere k
abbastanza grande. Ciò basta per concludere che la
funzione non è uniformemente continua.
Questa volta il motivo che rende la funzione non uniformemente continua va ricercato nel fatto che, al crescere di x, le oscillazioni diventano sempre più fitte, ed è questo che rende impossibile l'esistenza di un tubicino da far scorrere su tutto il grafico.
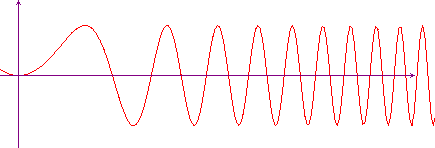
Si noti che, in questo caso, la funzione è limitata, a differenza di quanto succedeva nel primo esempio.
La funzione 
, di
I=[1,+∞[ in R, è continua in
tutto il dominio. Proviamo che essa é uniformemente
continua. Se x ed y sono due punti di I, si ha
. Fissato ε>0, basterà
allora prendere δ=ε per concludere. Si noti che
questa funzione non è limitata, eppure è
ugualmente uniformemente continua: il motivo è da
ricercare nel fatto che la velocità con cui la funzione
va all'infinito è molto bassa.
Teoremi sulle funzioni uniformemente continue
Come mostrano gli esempi sopra riportati, la verifica diretta della continuità uniforme non è sempre agevole: per fortuna esistono alcuni teoremi che facilitano il lavoro. Ci occuperemo ora dei più importanti, senza alcuna pretesa di completezza.
I seguenti teoremi esprimono condizioni sufficienti per
l'uniforme continuità.
Teorema di Heine-Cantor. Ogni funzione continua in un insieme chiuso e limitato di R è uniformemente continua.
Si tratta di uno dei risultati più importanti riguardanti le funzioni uniformemente continue. Si noti che esistono anche funzioni che sono uniformemente continue pur non essendo definite in insiemi non chiusi e limitati. Esempi classici sono le funzioni trigonometriche seno e coseno. Se la definizione di uniforme continuità si dà per funzioni tra spazi metrici generici (cosa possibile), allora l'insieme chiuso e limitato dell'enunciato di questo teorema va sostituito con "insieme compatto".
Teorema dell'asintoto. Ogni funzione continua di [a,+∞[ in R, dotata di asintoto orizzontale od obliquo è uniformemente continua.
Naturalmente esistono funzioni uniformemente continue senza asintoti orizzontali od obliqui, come per esempio le funzioni trigonometriche seno e coseno.
Teorema sulle funzioni Hölderiane. Le funzioni α-Hölderiane (e quindi anche le Lipschitziane) sono uniformemente continue.
Si noti che esistono funzioni uniformemente continue, ma non
Hölderiane, come per esempio: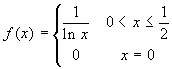 
.
Che questa funzione sia uniformemente continua è una
conseguenza della continuità e del teorema di
Heine-Cantor. Se essa fosse Hölderiana dovrebbero esiste un
α>0 e un H tali che 
.
Sia ora x=1/n e
y=1/n2, con n naturale
diverso da zero. Si avrebbe allora: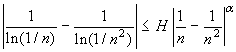 
,
ovvero 
, e quindi 
,
disuguaglianza impossibile per ogni n maggiore di zero,
perché il primo membro tende a +∞, mentre il
secondo tende ad H.
Funzioni con derivata limitata. Se una funzione ha derivata limitata in un intervallo I, allora è uniformemente continua in I.
Il viceversa non è vero, come prova la funzione 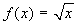che è
uniformemente continua in ]0,1] (per il teorema di Heine-Cantor
è uniformemente continua in [0,1] e quindi, a
fortiori, in ]0,1]), ma ha chiaramente derivata non limitata.
I seguenti teoremi esprimono condizioni necessarie per
l'uniforme continuità.
Teorema 1. Sia f : A → R una funzione uniformemente continua, con A limitato, allora f(A) è limitato.
Conseguenza di questo teorema è che le funzioni con asintoti verticali non possono essere uniformemente continue.
Teorema 2 (della farfalla). Sia f : [a,+∞[ → R una funzione uniformemente continua. Allora esistono due costanti positive m e q tali che |f(x)| ≤ m|x|+q.
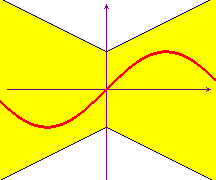
Il viceversa non è vero, come prova la funzione f(x) = sin(x2), che soddisfa la condizione precedente con m=0 e q=1, ma non è uniformemente continua.
Il nome del teorema deriva dal fatto che, se una funzione è uniformemente continua, la parte di piano che il suo grafico può occupare ha, appunto, la forma di una farfalla.
Da questo teorema segue che i polinomi di grado maggiore di 1 non possono essere uniformemente continui in R.
Teorema 3. Sia f : A →
R una funzione uniformemente continua e sia
c (R) un punto di accumulazione per
A. Allora esiste finito il 
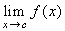. Inoltre la funzione
g definita sulla chiusura di A mediante il
valore dei limiti sui punti di accumulazione è
uniformemente continua. Si tenga presente che il teorema non
vale se c è infinito (si pensi alle funzioni
seno e coseno).
Questo teorema è di grande importanza perché afferma che una funzione uniformemente continua in un dato insieme può essere prolungata ad una funzione (uniformemente) continua sulla chiusura dell'insieme stesso.