Esercizi sulle funzioni integrali
Esercizio 1 Data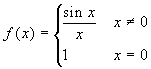 
, si
determinino le ascisse dei punti di massimo e minimo relativo
per la funzione 
.
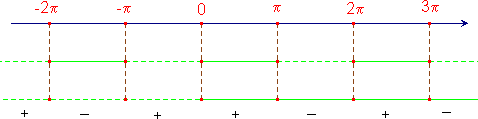
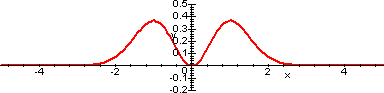
Basta osservare che F' = f su tutto R e trovare il segno di f. Per concludere basta osservare il grafico qui sotto.
.
Esercizio 2 Trovare il dominio delle
seguenti funzioni: 
.
La prima ha dominio x>0, la seconda x<0. Infatti per F a partire dal punto 1 si possono raggiungere solo i punti x dove la funzione f risulta limitata e quindi solo gli x positivi. Analogo discorso per G.
Esercizio 3 Data la funzione
g(t) =arctan2(t), si
consideri la funzione 
.
- Se ne trovi il dominio e si dimostri che è una funzione pari.
- Si dica se è possibile prolungarla per continuità ad una funzione definita su tutto R.
- Si dica se la funzione così prolungata è di classe C1(R).
- Si calcoli il limite di f, quando x tende a +∞.
1. Il dominio è chiaramente x≠0. Si ha poi
. Abbiamo operato il cambiamento di variabile
t = -s, che ha derivata -1 e abbiamo tenuto
conto che la funzione integranda è pari.
2. Calcoliamo il limite per x tendente a zero.
Scrivendo la funzione come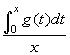 
, si vede subito che si
ha la forma indeterminata 0/0 per cui si può applicare la
regola di l'Hôpital. Si ottiene: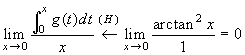 
. Per
prolungarla basta allora porre f(0) = 0.
3. Per x≠0 si ha 
, per cui 
. Questo basta per concludere che la funzione è
derivabile in 0 e la sua derivata è continua, ovvero
f è di classe C1(R).
4. Scrivendo la funzione come indicato al punto 2 si vede subito
che il limite richiesto si presenta nella forma ∞/∞,
per cui si può applicare la regola di
l'Hôpital. Si ottiene allora facilmente 
.
Esercizio 4 Dato il numero reale
α si consideri la funzione 
. Si
trovi il più grande valore di α per cui la funzione
è monotòna crescente. Detta
G l'inversa di F, per il valore di α
trovato, si trovi l'equazione della tangente al grafico di
G nel suo punto di ascissa 0.
Avendosi F'(x) =
gα(x), basterà trovare
α in modo che gα sia non
negativa. Si deve cioè trovare α in modo che la
disequazione 
sia sempre verificata. Tenendo conto
del grafico della funzione a primo membro, che è
rappresentato qui sotto, e del noto grafico di sinx, si
conclude che α deve essere ≤-1.
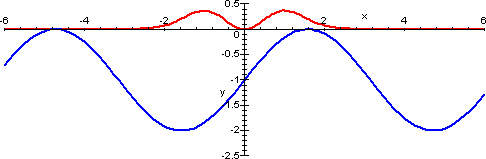
Il grafico dei due membri per α = -1 è rappresentato qui sotto.
La tangente all'inversa nel suo punto di ascissa 0 è
y = G(0) +
G'(0)·x. Si ha G(0)=0 e
. L'equazione richiesta è allora
semplicemente y = x.
Esercizio 5 Sia f una
funzione di classe C1(]0,+∞[). Mostrare che
f soddisfa la 
se e solo se è
costante.
Se f è costante 
, per cui la
condizione indicata è verificata. Supponiamo che,
viceversa, valga la condizione indicata. Allora 
.
Derivando membro a membro si trova 
. da
qui si conclude che f'(x)=0 in
]0,+∞[ e quindi che f è costante.