Integrale di Riemann - Qualche richiamo teorico
In questo sito abbiamo proposto anche una trattazione dettagliata dell'integrale di Riemann (in inglese). In questa pagina invece ci limitiamo a riportare solo alcune delle nozioni "tecniche" più utili per risolvere gli esercizi.
La funzione integrale
Ricordiamo che se f è una funzione integrabile secondo Riemann in un intervallo I e se
c
è un punto qualunque di I, allora risulta definita, per tutti gli x di I, la funzione
, detta
funzione integrale di
f, di punto iniziale c. Le funzioni integrale sono sempre continue, non appena
f è
integrabile, mentre risultano derivabili in tutti i punti dove f è continua. Se poi
f è
continua su tutto I, allora vale la famosa formula
, per ogni coppia di punti
a e b di I, dove F è una qualunque primitiva di
f.
Ricordiamo esplicitamente che una condizione necessaria per l'integrabilità secondo Riemann è che la funzione f sia limitata nell'intervallo I.
Riportiamo qui di seguito alcune tra le nozioni che interessano maggiormente le applicazioni delle funzioni integrali, limitandoci a considerare funzioni f continue in I.
- Se
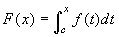, allora
F'(x) = f(x), per ogni x di I. - Se
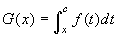, allora
G'(x) = -f(x), per ogni x di I. - Se g è una funzione derivabile in I, allora
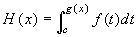è derivabile in I e
H'(x) =
f(g(x))·g'(x), per ogni
x di I. Naturalmente si richiede che
g(x) stia in I affinché l'integrale abbia senso. Questo fatto è una banale conseguenza
del teorema di derivabilità delle funzioni composte. - Se g e h sono funzioni derivabili in I, allora si può considerare la funzione
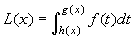, naturalmente purché
g(x) e
h(x) stiano in I. Questa funzione risulta derivabile e per calcolarne la derivata basta considerare un
qualunque punto c di I e osservare che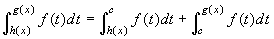
.