Esercizi solo con i limiti fondamentali
Esercizio 1 
(per il segno distingui k pari e
k dispari).
Esercizio 2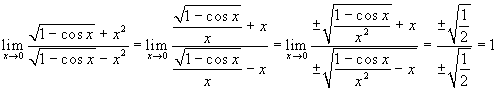 
(si
deve scegliere il segno + o il segno -, a seconda che si tratti
di limite destro o sinistro, ma il risultato è lo
stesso).
Esercizio 3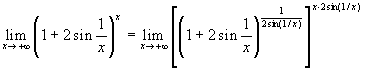 
. Per
calcolare questo limite osserviamo che si ha: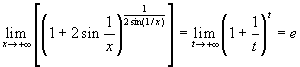 
, mentre 
. Il limite vale dunque
e2.
Esercizio 4 
. Per
calcolare 
abbiamo utilizzato il cambiamento di
variabile x-2 = t.
Esercizio 5 
.
Esercizio 6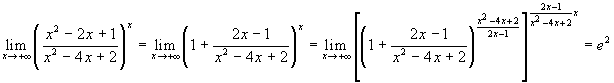 
. Il
limite tra parentesi quadre è del tipo 
.
Esercizio 7 
.
Esercizio 8 
. Per
concludere abbiamo osservato che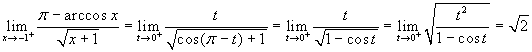 
.
Esercizio 9 
.
Esercizio 10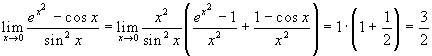 
.
Esercizio 11 
. Se
λ=0, il limite è, banalmente, +∞. Se
λ>0 la funzione 
oscilla tra -1 ed 1,
passando infinite volte per 0: il limite non esiste. Se
λ<0 si ha 
. Il primo fattore
tende a zero, mentre il secondo tende ad 1 (basta mettere
eλx = t). Il limite vale 0.