Limiti - Esercizi vari - 1
Esercizio 1
.
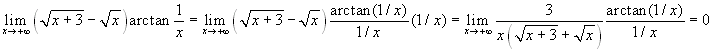Esercizio 2 Calcolare, al variare
di α>0: 
. Al numeratore ho la
somma di due infinitesimi; il primo ha ordine 6, il secondo
α+1. Allora:
- se α+1<6 (α<5) si trascura il primo;
- se α+1>6 (α>5) si trascura il secondo;
- se α+1=6 (α=5) si tengono entrambi.
Al denominatore si ha: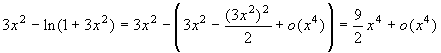 
. Esaminiamo ora i
tre casi:
-
α<5. Si ha:
.
-
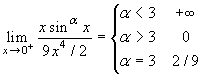α>5. Si ha:
.
-
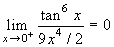α=5. Si ha:
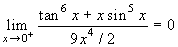(in ogni caso il
numeratore ha almeno ordine 6).
Esercizio 3 Calcolare, al variare
di α>0: 
. Usando Taylor e i
limiti fondamentali si trova: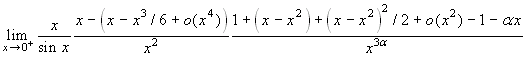 
. Eseguendo le
semplificazioni possibili si ha poi: 
. A
questo punto dobbiamo distinguere vari casi.
-
α=1:
.
-
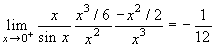α≠1:
.
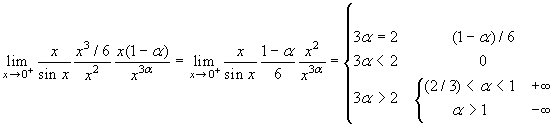Esercizio 4 Calcolare, al variare
di α>0: 
. Esaminiamo solo
l'esponente: 
. La prima e ultima
frazione tendono a 1 e -2. Rimane solo: 
. In
definitiva il limite vale: 
.
Esercizio 5 Calcolare, al variare
di α>0 e β il 
. Il numeratore ha
limite 1-β. Il denominatore è la somma di due
infinitesimi
- e-(1/x)lnx è infinitesimo di ordine maggiore di ogni potenza di x;
-
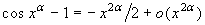, per cui il secondo infinitesimo
è di ordine 2α.
Al denominatore si può dunque trascurare il primo infinitesimo. Allora:
- se β>1, il limite è +∞ per ogni α;
- se β<1, il limite è -∞ per ogni α;
Esaminiamo poi il caso β=1. Se anche α=1: 
. Altrimenti possiamo scrivere: 
.
Rimane dunque: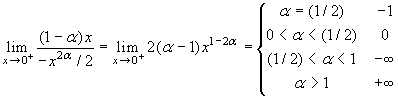 
.