Limiti - Esercizi vari - 2
Esercizio 1 Calcolare, al variare del
numero reale α, il ![]() . Il numeratore della
frazione tende a
. Il numeratore della
frazione tende a 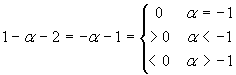 . Il denominatore tende
a
. Il denominatore tende
a 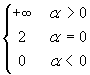 . Dunque:
. Dunque:
- se α>0 il limite si presenta nella forma (numero negativo)/∞, e il risultato è 0;
- se α=0 il limite è -1/2;
- se -1<α<0 il limite si presenta nella forma (numero negativo)/0+, e il risultato è -∞;
- se α<-1 il limite si presenta nella forma (numero positivo)/0+, e il risultato è +∞;
Rimane il caso α=-1 quando il limite si presenta nella
forma 0/0. Al denominatore si ha la somma di due infinitesimi,
di cui il primo è di ordine superiore al secondo, per cui
può essere trascurato. Il limite da calcolare diventa
dunque: ![]() . Per l'ultimo fattore si
può osservare che
. Per l'ultimo fattore si
può osservare che 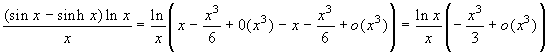 .
.
Esercizio 2 Calcolare, al variare del
numero reale α>0, il 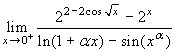 . Il numeratore si
può scrivere come
. Il numeratore si
può scrivere come 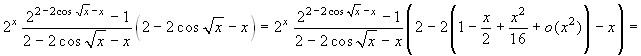
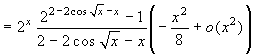 . Tenuto
conto che il primo fattore tende ad 1 e il secondo a ln2, ci si
può limitare a considerare il terzo. Per il denominatore
osserviamo che se α>1 il secondo addendo è
infinitesimo di ordine superiore al primo, per cui si può
trascurare; se α<1 il primo addendo è di ordine
superiore al secondo per cui si può trascurare; se invece
α=1 sono infinitesimi dello stesso ordine. Esaminiamo i
vari casi.
. Tenuto
conto che il primo fattore tende ad 1 e il secondo a ln2, ci si
può limitare a considerare il terzo. Per il denominatore
osserviamo che se α>1 il secondo addendo è
infinitesimo di ordine superiore al primo, per cui si può
trascurare; se α<1 il primo addendo è di ordine
superiore al secondo per cui si può trascurare; se invece
α=1 sono infinitesimi dello stesso ordine. Esaminiamo i
vari casi.
-
α>1.
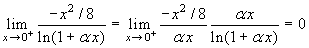 , e il limite vale 0.
, e il limite vale 0.
-
α<1.
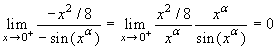 , e il limite 0.
, e il limite 0.
-
α<1.
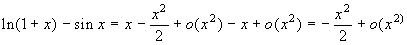 . Allora
. Allora 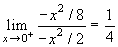 e il limite, in conclusione, vale ln2/4.
e il limite, in conclusione, vale ln2/4.
Esercizio 3 Calcolare, al variare del
numero reale α, il ![]() . Il denominatore si
può sostituire, usando i limiti fondamentali, con
xα+2. Se α=0 il numeratore si
riduce a cosx-1 e il limite vale -1/2. Se α≠0
al numeratore otteniamo:
. Il denominatore si
può sostituire, usando i limiti fondamentali, con
xα+2. Se α=0 il numeratore si
riduce a cosx-1 e il limite vale -1/2. Se α≠0
al numeratore otteniamo: 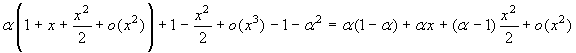 . Si devono dunque
distinguere il caso α≠1, in cui il numeratore ha limite
finito α(1-α), e quello α=1 in cui il
numeratore vale x+o(x2).
Si presentano le seguenti situazioni:
. Si devono dunque
distinguere il caso α≠1, in cui il numeratore ha limite
finito α(1-α), e quello α=1 in cui il
numeratore vale x+o(x2).
Si presentano le seguenti situazioni:
- α<-2. Il limite si presenta nella forma (numero negativo)/∞, e il risultato è 0;
- α=-2. Il limite vale -6 (il denominatore tende ad 1);
- -2<α<0. Il limite si presenta nella forma (numero negativo)/0+, e il risultato è -∞;
- α=0. Il limite vale -1/2, come già osservato;
- 0<α<1. Il limite si presenta nella forma (numero positivo)/0+, e il risultato è +∞;
- α=1. Il limite si riduce a x/x3, e tende a +∞;
- α>1. Il limite si presenta nella forma (numero negativo)/0+, e il risultato è -∞.
Esercizio 4 Calcolare, al variare del
numero reale α>0, il ![]() . Il limite
richiesto si può scrivere come
. Il limite
richiesto si può scrivere come ![]() . Il
primo fattore tende a 1. Esaminiamo il denominatore del secondo
fattore, che si presenta come somma di due infinitesimi, il
primo di ordine 1 e il secondo di ordine infrareale strettamente
minore di α. Allora se α>1 il secondo addendo si
può trascurare e il limite vale 1/3. Se invece
α≤1 si può trascurare il primo addendo e il
limite si presenta come il rapporto di due infinitesimi, di cui
quello al numeratore è di ordine superiore: il limite
vale 0.
. Il
primo fattore tende a 1. Esaminiamo il denominatore del secondo
fattore, che si presenta come somma di due infinitesimi, il
primo di ordine 1 e il secondo di ordine infrareale strettamente
minore di α. Allora se α>1 il secondo addendo si
può trascurare e il limite vale 1/3. Se invece
α≤1 si può trascurare il primo addendo e il
limite si presenta come il rapporto di due infinitesimi, di cui
quello al numeratore è di ordine superiore: il limite
vale 0.
Esercizio 5 Calcolare, al variare del
numero reale α, il ![]() . Il limite si
può trasformare in:
. Il limite si
può trasformare in: ![]() , che è della
forma 0/0 per ogni valore di α. Applichiamo la regola di
l'Hôpital. Si ottiene:
, che è della
forma 0/0 per ogni valore di α. Applichiamo la regola di
l'Hôpital. Si ottiene: 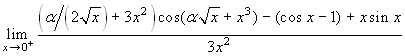 . Se
α≠0 il limite è +∞. Se α=0 il limite
si riduce a:
. Se
α≠0 il limite è +∞. Se α=0 il limite
si riduce a: ![]() .
.
Esercizio 6 Calcolare, al variare del
numero reale α, il ![]() . Il numeratore della
frazione tende a zero, mentre il denominatore tende ad
1-α. Quindi se α≠1 il limite vale 0. Se α=1
si può osservare che, al denominatore,
. Il numeratore della
frazione tende a zero, mentre il denominatore tende ad
1-α. Quindi se α≠1 il limite vale 0. Se α=1
si può osservare che, al denominatore, ![]() è infinitesimo di ordine 1/2, mentre
ex-1 è di ordine 1 e quindi si
può trascurare. Si ottiene allora:
è infinitesimo di ordine 1/2, mentre
ex-1 è di ordine 1 e quindi si
può trascurare. Si ottiene allora: ![]()
![]() .
.