Calcoli approssimati con la formula di Taylor
La formula di Taylor-Lagrange è molto utile per valutazioni approssimate in quanto permette, in molti casi, una semplice valutazione dell'ordine di grandezza dell'errore che si commette approssimando una funzione con un polinomio di Taylor di grado opportuno. Ricordiamo qui l'enunciato del teorema relativo.
Formula di Taylor-Lagrange: Sia f una funzione
definita in un intervallo I = ]a,b[ e sia c 
I. Supponiamo che in I la funzione sia derivabile
n-1 volte, mentre esiste anche la derivata
n-esima in I\{c}. Allora per ogni x
di I\{c} 
ξ tra x e c tale che: 
.
Si noti che, mentre nella formula di Taylor-Peano si hanno solo
informazioni sull'ordine di infinitesimo del resto (e per
questo essa è utile nel calcolo dei limiti), in questo
caso si ha una formula esplicita per il resto. Esaminando la
formula si può concludere che l'errore che si
commette approssimando, in un punto x di
]a,b[, una funzione con il suo polinomio di Taylor di
un certo grado p è, in valore assoluto,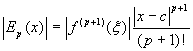 
, essendo ξ un valore compreso tra c
ed x, oppure tra x e c. Poiché
non è nota la posizione di ξ, non si può
valutare esattamente questo errore. Se però si riesce a
trovare il massimo, diciamolo M, di 
, allora l'errore sarà sicuramente minore di
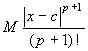. In molti casi invece di trovare il massimo si
trova una maggiorazione, che possiamo ancora indicare
con M, di e si conclude di nuovo,
anzi a maggiore ragione, che l'errore è sicuramente
minore di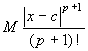 
.
Nelle applicazioni le richieste comuni sono qui di seguito elencate.
-
Fare in modo che l'errore, per un dato x, sia
minore di un prefissato valore, α (in genere molto
piccolo): basterà, in genere per tentativi, cercare
p in modo che 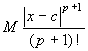sia minore di
α. Questa richiesta potrebbe anche essere formulata
così: fare in modo che il valore approssimato abbia un
determinato numero, m, di cifre decimali esatte, nel
qual caso basterà richiedere che l'errore sia
minore della metà di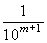
.
-
Valutare l'errore che si commette prendendo, per un
determinato valore di x, un'approssimazione
polinomiale di un certo grado. Basterà calcolare il
valore di 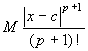, con p uguale al grado
dell'approssimazione richiesta. A volte può essere
richiesta solo una valutazione dell'errore massimo, a
volte una stima dell'errore comprendente un minimo ed un
massimo.
- Trovare un intorno del punto iniziale c nel quale l'approssimazione, per un dato n, non superi un valore prefissato, oppure sia compresa entro limiti prefissati.
Nella tabella che segue abbiamo riportato i polinomi di Taylor e i valori degli errori, cioè del valore assoluto del resto nella forma di Lagrange, per le funzioni elementari più importanti, con punto iniziale 0.
| Funzione | Polinomio di Taylor | Errore |
| sinx |
|
|
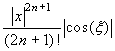
| cosx |
|
|
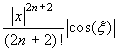
| ex |
|
|
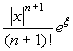
| sinhx |
|
|
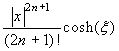
| coshx |
|
|
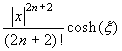
| ln(1+x), x > -1 |
|
|
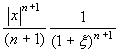
| (1+x)α, x > -1 |
|
|
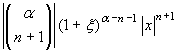
Per quanto riguarda le maggiorazioni sul resto si possono fare le osservazioni che seguono.
- Per le funzioni seno e coseno la maggiorazione è ovvia: |cos(ξ)| ≤1;
- La funzione esponenziale è strettamente crescente, per cui eξ raggiunge il suo massimo valore nell'estremo destro dell'intervallo. Se, per esempio, x=1/2, si ha eξ ≤ e1/2; a questo punto si può osservare che e1/2 ≤ e < 3, che ci consente di avere una maggiorazione espressa con numeri interi. In maniera analoga si ragiona per altri valori di x.
- La funzione coseno iperbolico è strettamente crescente per gli x positivi e strettamente decrescente per gli x negativi, per cui cosh(ξ) raggiunge il suo massimo valore nell'estremo destro o nell'estremo sinistro dell'intervallo. A questo punto si possono ripetere le considerazioni già fatte per la funzione esponenziale.
- Per gli ultimi due sviluppi basta tenere conto che la funzione 1/(1+t) è decrescente per t > -1, e poi ragionare come sopra.