Esercizi su approssimazioni con la formula di Taylor - 2
Esercizio 1 Valutare l'errore che si commette approssimando ln(3/2) con il polinomio di Taylor di ln(1+x) di grado n, con punto iniziale 0.
Il resto Rn(x) dello sviluppo di Taylor di
ln(1+x) è 
, essendo ξ un numero
compreso tra 0 ed x oppure tra x e 0; nel
nostro caso x = 1/2 e quindi 0 < ξ < 1/2.
Quindi 
. Se n è pari si ha 
(per cui il valore ottenuto trascurando il resto
è approssimato per difetto), mentre se n
è dispari si ha: 
(per cui il valore
ottenuto trascurando il resto è approssimato per
eccesso).
Esercizio 2 Se per calcolare sin(1/10) si usa il polinomio di Taylor di grado 5, quale errore si commette?
Si tratta di trovare una maggiorazione per il resto. Osserviamo
che il polinomio di grado 6 coincide, per il seno, con quello di
grado 5, per cui basterà trovare una maggiorazione per
R7(1/10). Si trova facilmente 
.
Esercizio 3 Calcolare 
,
con un errore minore di 10-4.
Da 
si ottiene il seguente sviluppo: 
. Integrando i due membri tra 0 ed 1 si può
ottenere il risultato voluto, pur di maggiorare opportunamente
l'integrale del resto. Si trova, facilmente, che 
. Questo numero vale 1/35280 se n = 3. Per
n = 3 l'errore soddisferà le ipotesi
richieste. Si può concludere che 
.
Esercizio 4 Calcolare il polinomio di
Taylor di grado 2 della funzione
esinx e valutare l'errore che
si commette approssimando la funzione con questo polinomio,
nell'intervallo 
. Per calcolare il
polinomio di Taylor di grado 2 si potrebbero utilizzare gli
sviluppi di ex e di sinx, ma
dovendo valutare l'errore calcoliamo le derivate successive
fino alla terza.
Si ha 
. Dunque f(0)=1,
f'(0)=1, f''(0)=1 e il polinomio
di grado 2 è: 
. Per maggiorare
l'errore osserviamo che sinx ≤ x, da cui segue
. Tenendo conto della forma del resto si conclude
che 
.
Esercizio 5 Calcolare 
con un errore inferiore a 10-7.
Dallo sviluppo di Taylor di et, di punto
iniziale 0, otteniamo 
. Siamo interessati a
porre t = -x2, per cui t
≤ 0. Allora t ≤ ξ ≤ 0, da cui
eξ ≤ 1. Se effettuiamo la sostituzione
t = -x2 e integriamo tra 0 ed 1/10
troviamo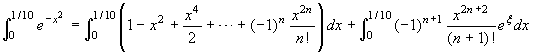 
. Si osserva poi che 
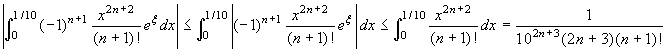. Basterà quindi trovare un n in modo che
l'ultimo termine sia minore di 10-7: n=2
è il più piccolo valore che soddisfa questa
richiesta. Ne segue che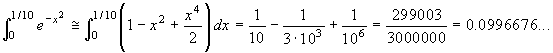 
.
Esercizio 6 Calcolare 
con un errore inferiore a 10-7.
Si possono ripetere le considerazioni dell'esercizio 5, solo
che ora bisogna trovare n tale che 
.
Utilizzando un programma di calcolo (es. Derive™ o
Mathematica™) si vede che il primo valore che soddisfa la
richiesta è n=33, un valore decisamente alto che
rende, tutto sommato, l'approssimazione polinomiale di
Taylor poco conveniente per il calcolo degli integrali.
D'altro canto si può osservare che
l'approssimazione in questione è, per costruzione,
"perfetta" localmente, cioè in un intorno del
punto iniziale, mentre può decisamente essere
"brutta" se ci allontaniamo dal punto iniziale. Nel
calcolo di un integrale, invece, il problema è quello di
un'approssimazione globale in un intervallo:
occorrerà applicare altri metodi. Solo per
curiosità riportiamo il valore approssimato
dell'integrale, ottenuto (ovviamente!!) con uno dei software
citati, 
: è chiaro che si tratta di una
tenica di nessuna utilità pratica.
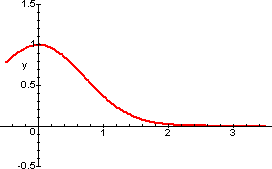
E' molto utile rendersi conto graficamente di quello che
succede, anche in relazione alla notevole differenza che
c'è rispetto all'esercizio precedente. Nelle
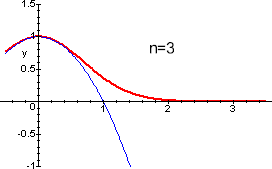
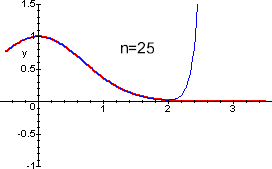
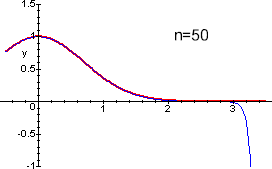
figure qui sotto si possono vedere i grafici di 
e dei polinomi di
Taylor di grado n=3, n=25, n=50, di
punto iniziale 0. Si vede subito che mentre nell'intervallo
[0,1/10] l'approssimazione globale è subito buona,
non altrettanto succede per l'intervallo [0,3].
|
|
|
|