www.batmath.it
Il grafico di asinx+bcosx
In questa pagina proponiamo una costruzione geometrica della funzione f(x) = asinx + bcosx. Questa funzione gioca un ruolo molto importante nelle applicazioni della trigonometria ed è bene, a nostro avviso, rendersi conto anche geometricamente, oltreché per via analitica, del suo andamento e del suo comportamento.
L'idea che sta alla base della costruzione è la seguente:
- si costruisce una circonferenza di centro l'origine e raggio a;
- con centro nel punto P di intersezione tra la circonferenza e il "secondo lato" dell'angolo x (in verde nella figura), si costruisce una seconda circonferenza di raggio b;
- il vettore in blu rappresenta il valore asinx, quello in verde il valore bcosx: la loro somma (vettoriale!) fornisce il valore asinx+bcosx: questa somma non è altro che l'ordinata del punto Q.
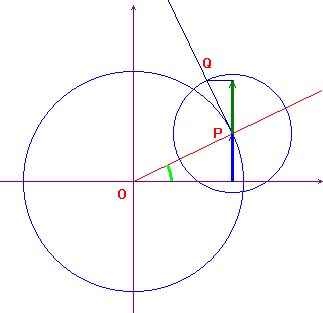
Si veda l'animazione qui sotto, dove l'ordinata di Q è riportata in una secondo sistema cartesiano, ottenendo così direttamente, al variare di x, il grafico richiesto.
copyright 2000 et seq. maddalena falanga & luciano battaia
pagina pubblicata il 24/02/2003 - ultimo aggiornamento il 01/09/2003