Il teorema del coseno (o di Carnot)
Questo famoso teorema, che costituisce una estensione del teorema di Pitagora ai triangoli non rettangoli, porta impropriamente il nome di Lazare Carnot (1753-1823), personaggio di spicco nel periodo della rivoluzione francese e del successivo impero di Napoleone, di cui fu dapprima nemico e successivamente apprezzato generale.
Il teorema, seppure in altra forma, era già noto ad Euclide, che vi dedica le Proposizioni 12 e 13 del Libro II: la prima relativamente ai triangoli ottusangoli (in cui il quadrato costruito sul lato opposto all'angolo ottuso è maggiore della somma dei quadrati costruiti sugli altri due lati) e la seconda relativamente ai triangoli acutangoli (in cui invece il quadrato costruito su un lato è sempre minore della somma dei quadrati costruiti sugli altri due).
Anche nella sua "forma trigonometrica" il teorema era noto molto prima di Carnot. Già usato dal matematico arabo-persiano al-Biruni (973-1048), si trova in Opera di Viéte (1540-1603), che lo enuncia nella forma:
2ab : (a2+b2-c2) = 1 : sin(90° - γ).
Lazare Carnot lo riporta in De la corrélation des figures en géométrie, del 1800-01 (anno IX); in Géométrie de la position (1803) stabilisce il teorema delle proiezioni, da cui poi ricava il teorema del coseno, nella forma oggi usata.
Anche Bonaventura Cavalieri, in Trigonometria plana et sphaerica, linearis et Logarithmica del 1643, lo riporta, completo di dimostrazione.
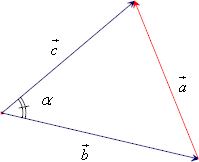
In termini moderni la dimostrazione può essere ottenuta in modo elementare utilizzando il calcolo vettoriale.
Se si esamina la figura qui sotto, si ottiene facilmente: ![]() , da cui
, da cui ![]() .
.
In questa pagina vogliamo proporre una dimostrazione di tipo grafico, che evidenzi le analogie e le differenze con il teorema di Pitagora, di cui il teorema del coseno può essere considerato una generalizzazione. La dimostrazione è, sostanzialmente, la visualizzazione grafica delle Proposizioni di Euclide.
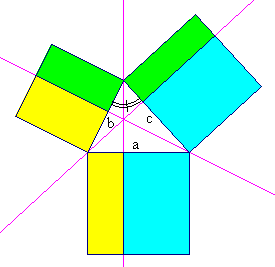
Esattamente come fa Euclide, distinguiamo il caso del triangolo acutangolo da quello del triangolo ottusangolo.
Per il triangolo acutangolo il quadrato costruito sul lato a è più piccolo della somma dei quadrati costruiti sui lati b e c. Nella figura qui sotto i rettangoli con lo stesso colore sono equivalenti, come si può vedere con l'animazione proposta più sotto; in particolare l'area dei due rettangoli verdi è: bccosα. Con questo il teorema è provato.
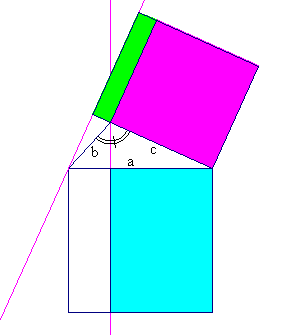
Per il triangolo ottusangolo il quadrato costruito sul lato a è più grande della somma dei quadrati costruiti sui lati b e c. Nella figura qui sotto, in cui abbiamo riportato per semplicità solo una parte della costruzione, il rettangolo celeste è la somma del quadrato lilla e del rettangolo verde. L'area del rettangolo verde è: - bccosα (bisogna tenere conto che l'angolo α è ottuso, quindi con coseno negativo). Con questo il teorema è provato.
L'animazione qui sotto costituisce una verifica "a vista" del teorema, in quanto mostra, per successive deformazioni e rotazioni che non modificano l'area, l'equivalenza dei rettangoli che intervengono nella dimostrazione.