Identità varie
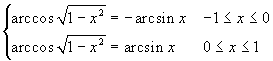. Per la dimostrazione si esamini la figura qui
sotto.
.
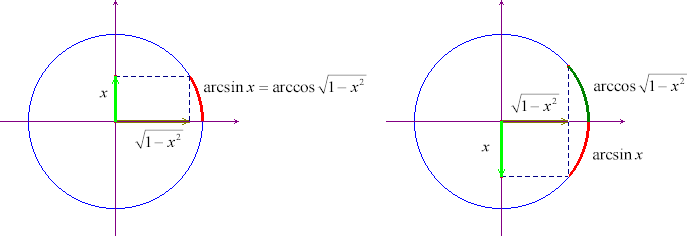
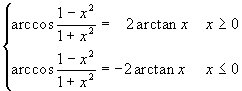Per la dimostrazione si esaminino le figure qui sotto, riferite la prima al caso x positivo, la seconda al caso x negativo. Si tratta di determinare la ascissa del punto Q, a partire dalle coordinate di T. Nel primo caso si trova subito, posto AÔP=α che xQ=cos2α=cos2α-sin 2α. Ma l'angolo α non è altro che arctanx e, tenendo conto delle note formule per il seno e il coseno di asctanx, si deduce subito la formula richiesta.
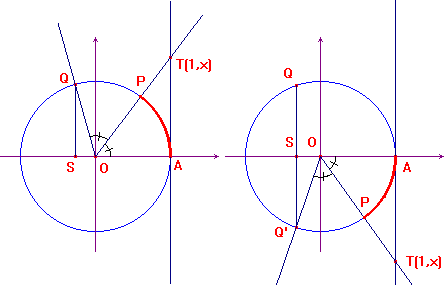
Nel caso di x negativo basta tenere conto, per concludere, della discordanza di segno tra arctanx, che è negativo, e l'arccoseno, che invece deve essere positivo.
. Per la dimostrazione si esaminino le due figure
qui sotto, di cui quella a sinistra si riferisce al caso
x positivo e quella a destra al caso x
negativo. Il numero reale x è l'ordinata del
punto C, l'arco AB è arcsinx, E è il
punto medio dell'arco AB e infine l'angolo QÔE
è di π/4. Si tratta in sostanza di trovare
l'ordinata del punto Q.
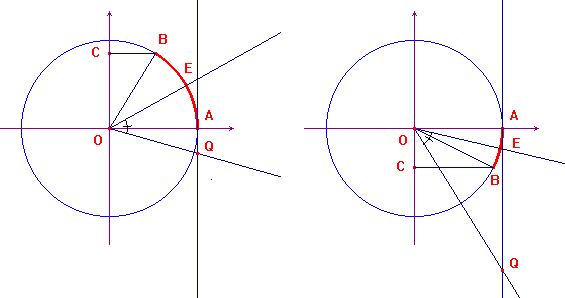
Ci limitiamo al caso rappresentato nella figura di sinistra,
lasciando al navigatore, per esercizio, di trattare l'altro.
Si comincia con l'osservare che qualunque sia x
nell'intervallo [-1,1], il punto Q sta nel quarto quadrante,
per cui si ha: yQ=-AQ. L'esame del
triangolo AÔQ dà, facilmente,
AQ=OAtan(AÔQ)=tan(AÔQ). L'angolo AÔQ vale
π/4-(arcsinx)/2. Tenendo conto delle formule di
addizione e di bisezione della tangente (queste ultime nella
forma 
), si ottiene, successivamente: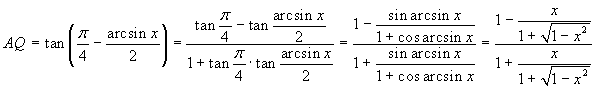 
. Si può razionalizzare e semplificare
ottenendo: 
. Questo basta per
concludere.