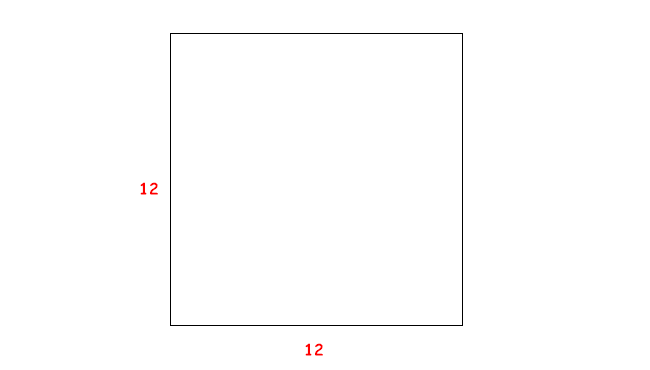
12 X 12 fa 144 o 145 ?
Il paradosso di cui si parla in questa pagina è noto come il quadrato di Curry, dal nome del suo inventore, un illusionista dilettante di New York. Ha numerose varianti e oggi si trovano in commercio anche costruzioni simili ai puzzle che riproducono paradossi di questo tipo.
Il problema si può così sintetizzare: dato un quadrato di lato 12, è possibile scomporlo in parti che, rimescolate e successivamente ricomposte occupino di nuovo un quadrato di lato 12, lasciando però un foro quadrato di lato 1?. La risposta, dal punto di vista matematico, è, ovviamente, negativa.
Ma provate a guardare la sequenza di immagini che si ottiene seguendo i passi indicati qui sotto.
|
|
|
|
|
|
|
|
| uno | due | tre | quattro | cinque | sei | sette |