Calcolatrici e frazioni: un connubio non sempre felice
Sempre più spesso si fanno i calcoli con le calcolatrici (d'altronde se le calcolatrici non venissero usate per fare calcoli, a che cosa servirebbero?), senza preoccuparsi di controllare l'attendibilità del risultato ottenuto. E non vogliamo qui riferirci agli errori di battitura (comunque sempre frequenti!), quanto piuttosto a limitazioni intrinseche nell'uso degli strumenti automatici di calcolo: i problemi legati alla "finitezza" di questi strumenti sono ben noti agli studiosi, ma spesso vengono ritenuti irrilevanti nei calcoli fatti dai "comuni mortali".
Per renderci conto di come stanno le cose proviamo ad impostare
su una calcolatrice il calcolo che segue. Poiché 
fa 
, se moltiplichiamo il risultato ancora
per 4 e sottraiamo 1, dovremmo ottenere sempre : 
. Se anche continuiamo nel
procedimento quante volte vogliamo dovremmo ottenere sempre : 
.
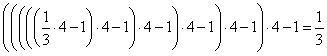Proviamo ad impostare questo calcolo su una calcolatrice. Il
calcolo da impostare è: 
. A questo punto
basta, senza cancellare il risultato ottenuto sul display,
ripetere un certo numero di volte la seguente sequenza di
operazioni: 
. Si noterà che, per un po',
sul display appare sempre il numero 
(il
numero di cifre dopo la virgola dipende dal tipo di calcolatrice
usata); ad un certo punto il risultato sul display comincia a
cambiare e, cosa ancora più interessante, il risultato, a
parità di numero di passi, cambia a seconda della
calcolatrice. Nella tabella che segue sono riportati i valori
ottenuti su tre calcolatrici dopo 10, 20, 30 passi.
| SHARP EL531LH | CASIO fx 4500P | CASIO fx3900PV | |
| 10 | 0.333332459 | 0.333245952 | 0.333324595 |
| 20 | -0.582926356 | -91.29263564 | -8.829263565 |
| 30 | -960767.5872 | -96076791.68 | -9607678.87 |
Come si può facilmente notare, dopo 10 passi i tre
risultati non differiscono di molto tra di loro e sono ancora
"abbastanza uguali" ad ; dopo
20 o 30 passi i tre risultati sono completamente diversi ed in
ogni caso molto distanti dal valore .
Come si spiega questo fatto, a prima vista sorprendente?. Tutto
è legato al fatto che la calcolatrice è costretta
ad approssimare il numero (che è
decimale periodico) prendendo solo un certo numero di cifre dopo
la virgola, e questo numero di cifre cambia a seconda della
calcolatrice (anche se ce ne vengono mostrate solo 8 o 10 sul
display, in realtà la calcolatrice, al suo interno, ne
usa molte di più). Per rendercene conto supponiamo che la
calcolatrice usi solo due cifre dopo la virgola e proviamo a
fare il conto "a mano", approssimando
con 0.33 (in fondo non è un grosso errore, si tratta solo
di circa 3 millesimi in meno!) in modo da avere solo due
decimali. Otteniamo:
| 1 | 0.32 | 2 | 0.28 | 3 | 0.12 | 4 | -0.52 | 5 | -3.08 | 6 | -13.32 | 7 | -54.28 | 8 | -218.12 | 9 | -873.48 | 10 | -3494.92 |
Si vede subito che, già dopo tre passi, il risultato è completamente sballato.
I problemi che derivano dall'uso dei "numeri approssimati" negli strumenti automatici di calcolo sono molto complessi e spesso difficili da trattare: si pensi che un normale calcolatore può fare milioni di operazioni al secondo e, dato che usa sempre numeri approssimati, si può ben capire a quali rischi si vada incontro.