Qualche strana funzione esponenziale
Proponiamo in questa pagina alcune funzioni esponenziali non usuali, volutamente patologiche, con il relativo grafico. Esse possono essere utili per aiutare a comprendere le difficoltà connesse col concetto di potenza nei reali.
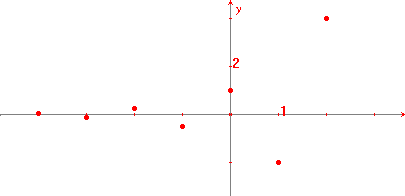
Esempio 1: studiare la funzione f(x) = (-2)x.
Poiché le potenze con base negativa sono definite solo per esponenti interi (positivi o negativi), il dominio di questa funzione è costituito solo dagli elementi di Z, e il suo grafico è il seguente:
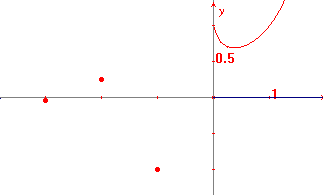
Esempio 2: studiare la funzione f(x) = xx.
Ragionando come nell'esempio 1 si vede che la funzione è definita per tutti gli x>0 e per tutti gli interi strettamente negativi. Il suo grafico, per gli x positivi, non è banale, mentre per gli x negativi può essere ottenuto facilmente per calcolo diretto.
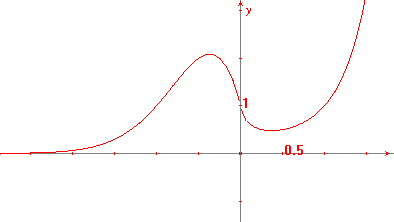
Esempio 3: studiare la funzione f(x) = (x2)x.
Questa funzione è definita per tutti gli x diversi da zero, in quanto la base della potenza, tranne che per x=0, è strettamente positiva. Il suo grafico, che non si può ottenere con metodi elementari, è riportato qui sotto.
Esempio 4: studiare la funzione f(x) = x(2x).
Questa funzione differisce da quella dell'esempio 3 per il
dominio, in quanto questa volta la base (che non è
elevata al quadrato), non è sempre positiva. Per gli
x positivi non si ha alcuna differenza con
l'esempio 3; per gli x negativi essa risulta
definita solo quando 2x è intero, ovvero quando
x = a/2, con a intero negativ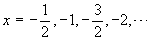o: 
. . Il suo
grafico, per alcuni valori negativi, è rappresentato qui
sotto.
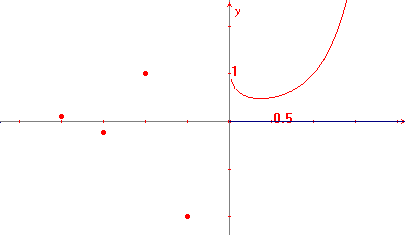
Si noti, confrontando gli esempi 3 e 4, che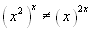 
.
Naturalmente, per fortuna, non tutte le funzioni che coinvolgono le potenze sono così patologiche!
