Considerazioni sull'insieme dei radicali

Lo spazio dedicato allo studio dei radicali nella scuola media superiore è, a nostro avviso, assolutamente spropositato in relazione all'importanza sia teorica che pratica dell'argomento. Mancano invece, abitualmente, alcune considerazioni che riteniamo di grande importanza.

Che cosa si intende in genere con radicale? Il concetto nasce dalla necessità di risolvere equazioni del tipo xⁿ = b, ove n è un numero naturale maggiore di 1 e b è un numero reale positivo (il caso di b negativo, con n dispari, crea solo problemi e preferiamo evitarlo, almeno in queste considerazioni informali). Come è noto con la scrittura 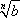si indica l'unica soluzione (positiva se n è pari) dell'equazione proposta (se n è pari l'equazione proposta ha in realtà due soluzioni opposte e precisamente ±).

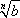La definizione più naturale di radicale è dunque quella di un numero reale del tipo 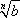, essendo b un numero reale positivo. Nelle applicazioni ha però interesse solo il caso che b sia un numero razionale e si usa di solito il termine radicale solo per oggetti di questo tipo più ristretto. In considerazione della nota proprietà 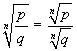, ci si può addirittura ridurre a chiamare radicali solo gli oggetti del tipo 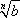, ove b è un intero positivo, e così faremo noi nel seguito.

La cosa importante relativa all'insieme dei radicali, considerati come sottoinsieme dei reali, è che questo insieme non è chiuso rispetto alle quattro operazioni, in particolare rispetto all'operazione di somma. Ci si può facilmente rendere conto di questo fatto considerando il seguente

Esercizio: Provare che non esiste un intero positivo a, tale che .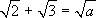

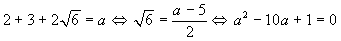Se un a come richiesto esistesse si avrebbe: . E' immediato che l'ultima equazione non ha soluzioni intere. Anche se è un po' più difficile si potrebbe anche provare che non esiste nemmeno a positivo tale che .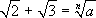

Dunque non si potrà mai sperare di semplificare un'espressione contenente le quattro operazioni con radicali in modo da ottenere un semplice radicale. La cosa è completamente diversa con il caso delle frazioni: qualunque espressione contenente le quattro operazioni con frazioni può sempre essere semplificata ad un  frazione.

E allora a che cosa serve insistere così tanto sui radicali? Verrebbe da rispondere: a poco o, meglio ancora, a nulla.

C'è però una osservazione da fare. Consideriamo l'espressione 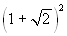e supponiamo di voler approssimare 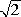con due cifre decimali esatte, ovvero con 1.41. Possiamo eseguire l'approssimazione prima di svolgere il quadrato, oppure dopo, ottenendo, rispettivamente:

1. approssimazione prima: ;
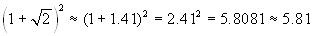2. approssimazione dopo: .

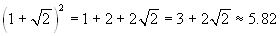Come si nota, dopo un solo passaggio si ha già una differenza di approssimazione sulla seconda cifra decimale. Con un po' di pazienza, e una calcolatrice a disposizione, si può facilmente vedere che la seconda approssimazione è migliore della prima: un calcolo con più cifre fornisce infatti il seguente risultato: 5.828427125...

E' questo il motivo vero per cui si imparano ad eseguire certe semplificazioni sui radicali: è meglio, in espressioni che li contengono, ridursi a forme semplici e in particolare contenenti solo somme, in quanto così gli errori di approssimazione non si ingigantiscono troppo. Per questo, per esempio, si studiano le famigerate razionalizzazioni del denominatore.

Per un giusto equilibrio sarebbe però da tenere presente che, anche con tecniche molto sofisticate, non si riesce quasi mai nell'intento di ridursi ad espressioni contenenti solo somme. Provate a razionalizzare 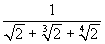, se non ci credete!

Allora: Adelante si con i radicali, ma con juicio!