Limiti di funzioni e grafici
Le rappresentazioni grafiche, sia per introdurre il concetto di limite, che per valutare i limiti stessi sono sempre state utilizzate estesamente, per ovvi motivi didattici. Con l'avvento dei computer è diventato quasi obbligatorio sfruttare le loro capacità, fino quasi ad abbandonare completamente la trattazione teorica del concetto di limite, per appoggiarsi solo alla visualizzazione.
Se è naturale sfruttare al meglio le capacità offerteci dalla moderna tecnologia, non dobbiamo però dimenticare i limiti di un approccio sostanzialmente basato solo su tecniche grafiche. Proponiamo alcuni esempi per evidenziare i tranelli in cui si può cadere, se si prende per oro colato quello che il computer ci mostra.
Supponiamo di voler valutare il limit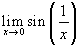e 
. Apriamo il
nostro programma preferito di grafica (qui abbiamo usato
Mathematica, ma vanno bene tutti) e in men che non si dica
riusciamo ad ottenere la seguente immagine
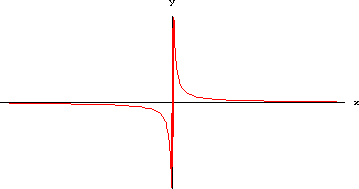
Tutti contenti per la semplicità del risultato ottenuto, concludiamo che il limite richiesto pare essere ∞ (per essere precisi -∞ a sinistra e +∞ a destra): del resto questo grafico non è molto diverso da quello, ben noto, dell'iperbole. Qualche sospetto ci viene però quando, all'improvviso, ci ricordiamo che la funzione seno è sempre compresa tra -1 e 1, per cui non può andare all'infinito. Ritornati al nostro software di grafica analizziamo meglio il problema e chiediamo di stampare anche una scala sull'asse delle ordinate. Otteniamo il nuovo grafico:
Adesso si che possiamo stare tranquilli: il limite richiesto non esiste, perché é -1 da sinistra e +1 da destra.
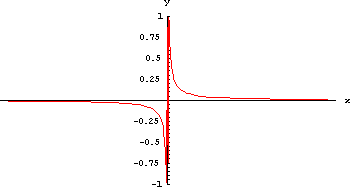
Proviamo invece a tornare a Mathematica e a fare qualche altra modifica. Per esempio facciamo uno zoom sull'asse x, magari facendoci stampare anche la scala su quest'asse. Otteniamo, con ingrandimenti diversi, i seguenti risultati:
Lasciamo al navigatore il compito di interpretare il risultato, tenendo conto che la funzione considerata è tra quelle che si analizzano più spesso nell'introduzione al concetto di limite.
Negli esempi che seguono, col proposito di trovare i limiti indicati, mostriamo due grafici con scale diverse per ogni caso, senza commenti e senza l'indicazione della scala. Per ogni coppia di grafici la scala sull'asse delle y è identica.
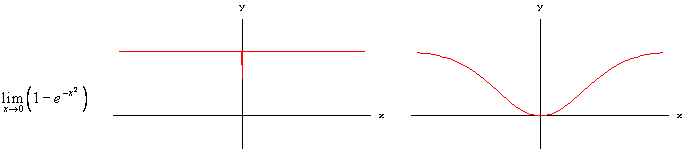
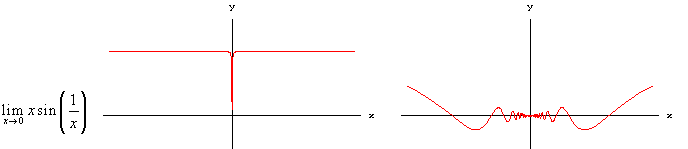
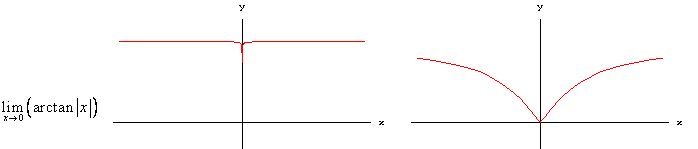
Come si vede facilmente, anche funzioni completamente diverse possono avere andamenti sostanzialmente identici, se esaminate a scale opportune!
Per evitare che a qualcuno possa venire in mente che, magari con opportuni zoom, qualsiasi problema di limite possa essere risolto per via grafica, vi invitiamo a guardare l'esempio di una funzione particolarmente discontinua.
