www.batmath.it

Il lavoro per una forza variabile in una dimensione

N.B. I concetti esposti in questa pagina sono adatti per una terza liceo scientifico e in generale per una classe dove non si è assolutamente parlato di integrali o derivate, pertanto il linguaggio utilizzato è del tutto informale.

Richiamiamo la definizione (a livello elementare) di lavoro per una forza F:

1. se la forza F è costante e il suo punto di applicazione si sposta da un punto iniziale A ad un punto finale B, in linea retta, 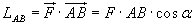, ove α è uno dei due angoli tra il vettore forza e il vettore AB (abitualmente si conviene di scegliere il minore dei due: in ogni il coseno è lo stesso, e nemmeno il verso dell'angolo è importante).
2. se la forza F non è costante oppure il suo punto di applicazione si sposta da un punto iniziale A ad un punto finale B non seguendo un percorso rettilineo, ma una curva γ, si approssima la curva con una spezzata, i cui lati saranno genericamente indicati con Δl, in modo tale che
   • l'approssimazione della curva con la spezzata sia "accettabile" dal punto di vista geometrico,
   • la forza F rimanga sostanzialmente costante su ognuno dei lati della spezzata;
   a questo punto, indicando con F_i il valore costante della forza sui vari lati della spezzata, si calcola il lavoro relativamente a ciascun lato e poi si sommano i contributi, .

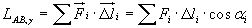E' ovvio che l'approssimazione è tanto migliore quanto più i lati della spezzata sono "piccoli", al limite "tendenti a zero": in questo caso useremo i simboli dl al posto di Δl, e ∫ al posto di ∑: 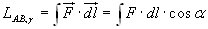. In sostanza l'approssimazione equivale a sostituire la linea curva con una spezzata e ad immaginare che la forza anziché variare con continuità lungo la curva, vari solo in corrispondenza del passaggio da un lato all'altro della spezzata.

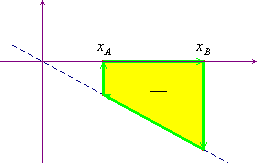
Consideriamo ora la situazione particolarmente interessante che il sistema (forze e spostamenti) sia unidimensionale e che la forza dipenda solo dalla posizione del suo punto di applicazione. Introdotto un sistema di ascisse sulla retta dove agisce la forza e dove si muove il suo punto di applicazione, indichiamo con F_x la componente della forza (che sarà uguale a ±F) e con dx la componente dello spostamento relativo al generico lato della spezzata. Il lavoro sarà allora ∫F_xdx. Rappresentiamo graficamente in un sistema cartesiano la componente F_x della forza in funzione della posizione e indichiamo rispettivamente con x_A e x_B l'ascissa iniziale e finale del suo punto di applicazione (immaginiamo per semplicità che x_A sia minore di x_B e che il punto si sposti lungo il segmento AB, senza "andare avanti e indietro"). Non è difficile rendersi conto che, in questo caso, il lavoro lungo un generico tratto della spezzata è dato dall'area di un rettangolo come quelli della figura qui sotto, presa con il segno se la componente della forza (su quel tratto di spezzata) è positiva (rettangolo giallo), con il segno meno se la componente della forza è negativa (rettangolo verde).

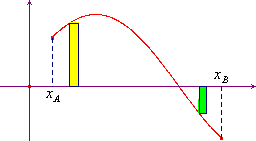
Per avere il lavoro totale basterà fare la somma di tante aree tipo quelle indicate ed è evidente che se i rettangoli in questione hanno una base "quasi uguale a zero", l'area da considerare tenderà a confondersi con quella compresa tra la curva che rappresenta al forza e l'asse delle x, presa con il segno più se la curva "sta sopra" l'asse delle x, con il segno meno in caso contrario. Si osservi anche che, se lo spostamento avviene da B ad A occorrerà cambiare soltanto i segni.

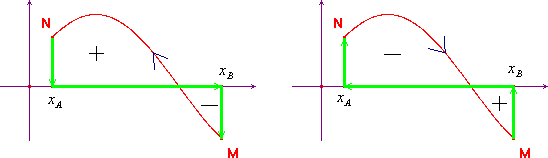
In generale si può concludere con la seguente regola, rappresentata nelle figure qui sotto: Si consideri il percorso chiuso dall'ascissa iniziale, all'ascissa finale, al punto (M o N) sul grafico della forza, poi lungo il grafico, ed infine dal punto (N o M) sul grafico della forza di nuovo all'ascissa finale. Questo percorso racchiude un certo numero di regioni nel piano cartesiano, alcune con il bordo percorso in senso antiorario, alcune con il bordo percorso in senso orario: il lavoro sarà la somma di tutte le aree delle regioni con il bordo antiorario, meno la somma di tutte le aree delle regioni con il bordo orario.

Particolarmente interessante il caso della forza elastica in cui il grafico di F_x (=-kx) è una retta passante per l'origine (con coefficiente angolare negativo): il lavoro è facilmente calcolabile perché le aree in questione si riducono a trapezi rettangoli o a triangoli. Se si esamina la figura qui sotto si trova: 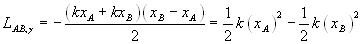 . Questa espressione è valida in generale.

copyright 2000 et seq. maddalena falanga & luciano battaia

pagina pubblicata il 25/02/2005 - ultimo aggiornamento il 25/02/2005