Preparazione all'esame di Stato (Liceo Scientifico) e ai test
di ammissione all'Università
Test a risposta multipla
Individua la risposta esatta
-
Quali delle seguenti uguaglianze è sempre vera?
lnx2 = 2lnx e (lnx)2 = ln(lnx)
-
solo la prima
-
solo la seconda
-
entrambe
-
nessuna delle due
-
Le due disequazioni 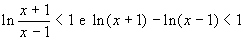
-
hanno lo stesso insieme di soluzioni
-
hanno insiemi di soluzioni disgiunti
-
sono tali che uno dei due insiemi di soluzioni
è sottoinsieme dell'altro
-
hanno lo stesso dominio
-
La disequazione sinx + cosx > 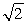
-
non ha soluzioni in R
-
è verificata per
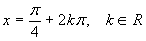
-
è verificata per
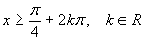
-
è verificata per
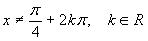
-
La successione 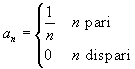
-
ha limite 0
-
non ha limite
-
è monotòna decrescente
-
La funzione inversa della funzione f(x) =
2x - 1 è
-
g(x) = 1/(2x - 1)
-
g(x) = 2x + 1
-
g(x) = (x + 1)/2
-
g(x) = (x - 1)/2
-
La funzione f(x) = 2x3 -
3x2
-
è pari
-
è dispari
-
è sempre positiva
-
è definita su tutto R
-
Le due funzioni 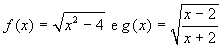
-
hanno lo stesso dominio
-
hanno gli stessi zeri
-
non sono definite per x=0
-
sono entrambe pari
-
Le funzioni f(x) = sinx e g(x) =
tanx
-
hanno lo stesso minimo periodo
-
sono entrambe dispari
-
hanno lo stesso dominio
-
hanno entrambe limite finito se x
tende a π/2
-
Date le funzioni f(x) = x2 + 2 e
g(x) = sinx, la funzione composta
f(g(x)) è:
-
sin(x2 + 2)
-
sin2x + 2
-
sin2(x + 2)
-
sin(x2) + 2
-
Date le funzioni f(x) = ln(x-2)2
e g(x) = 2ln(x-2), vale la seguente
proprietà:
-
hanno lo stesso dominio ma diverso insieme
immagine
-
la prima è sempre positiva, la seconda
no
-
hanno lo stesso insieme immagine
-
hanno lo stesso dominio e lo stesso insieme
immagine
-
Il dominio della funzione 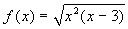 è:
è:
-
x ³
3
-
R
-
x = 0
-
x = 0
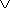 x ≥ 3
x ≥ 3
-
x = 0
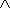 x ≥
3
x ≥
3
-
Le funzioni f(x) = cos(x2) e
g(x) = (cosx)2
-
hanno entrambe periodo 2π
-
sono entrambe sempre positive
-
sono entrambe pari
-
sono entrambe dispari
-
Quale delle seguenti funzioni reali è invertibile nel
suo dominio naturale (eventualmente con una restrizione sul
codominio)?
-
x2
-
1/(x2)
-
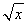
-
sinx
-
tanx
-
Il grafico della funzione 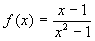
-
ha due asintoti verticali e nesuno orizzontale
-
ha un asintoto verticale e uno orizzontale
-
ha due asintoti verticali e uno orizzontale
-
ha un asintoto obliquo
-
Il 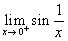
-
vale 0
-
vale 1
-
vale +∞
-
non esiste
-
Il 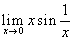
-
vale 0
-
vale 1
-
vale +∞
-
non esiste
-
Di una funzione f, definita in tutto R, si sa
che, per x <0, 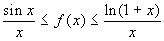 . Si può
affermare che
. Si può
affermare che 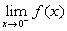 vale
vale
-
1
-
0
-
2
-
non esiste
-
non si hanno dati per concludere
-
Se una funzione ha, in un punto c, limiti destro e
sinistro diversi, si può affermare con certezza che
-
la funzione non può essere continua in
c
-
la funzione ha in c un salto finito
-
la funzione ha in c un salto infinito
-
la funzione non è limitata in un
intorno di c
-
Se in un punto c la funzione f(x) + g(x)
è derivabile, allora
-
nel punto c le due funzioni
f e g sono derivabili
-
nel punto c almeno una delle due
funzioni f e g è derivabile
-
nel punto c le due funzioni
f e g sono continue
-
nulla si può dire riguardo la
continuità delle due funzioni nel punto c
-
Se una funzione è derivabile in un intervallo aperto U
la condizione che f'(c) = 0 in un punto
c di U
-
è sufficiente per l'esistenza di un
punto di massimo o minimo in c
-
è necessaria e sufficiente per
l'esistenza di un punto di massimo o minimo in
c
-
è necessaria ma non sufficiente per
l'esistenza di un punto di massimo o minimo in
c
-
non è necessaria per l'esistenza di
un punto di massimo o minimo in c
-
Per quali valori di k la funzione f(x) =
k|x| è derivabile per x = 0?
-
k = 0
-
k > 0
-
k < 0
-
per nessun valore di k
-
La derivata della funzione f(x) =
sinxcosx è
-
cos(2x)
-
-cos(2x)
-
-sin(2x)
-
sin(2x)
-
La funzione 
-
ha derivata nulla nel suo dominio naturale
-
è sempre negativa
-
è sempre positiva
-
è costante nel suo dominio naturale
-
Un'equazione di terzo grado in un'incognita reale
-
ha sempre tre soluzioni reali (eventualmente
non distinte)
-
ha sempre almeno una soluzione reale
-
può non avere alcuna soluzione reale
-
ha sempre almeno due soluzioni reali
-
Se due funzioni sono derivabili in R allora, per ogni
x di R si ha
-
f'(x) = g'(x)
 f(x) = g(x)
f(x) = g(x)
-
f(x) = g(x)
 f'(x) = g'(x)
f'(x) = g'(x)
-
f(x) ≥ g(x)
 f'(x) ≥ g'(x)
f'(x) ≥ g'(x)
![]()
![]()
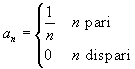
![]()
![]() è:
è:
![]()
![]()
![]()
![]() . Si può
affermare che
. Si può
affermare che ![]() vale
vale
![]()