Continuity in intervals
Definition and examples
A function is called continuous in a subset A of the domain D, if it is continuous at all points in A. We are strongly interested about the case where A is an interval, especially a closed and bounded interval: we shall call this kind of intervals compact intervals.
Functions continuous in compact intervals have two very important properties:
- The max-min theorem. Suppose a function f is continuous in the closed interval [a,b]. Then there exist real numbers x1 and x2 such that f(x1) is the minimum value, m, and f(x2) is the maximum value, M, of f in the interval.
- The intermediate value theorem. Suppose a function f is continuous in the closed interval [a,b]. Then for every real number y satisfying f(x1)≤y≤f(x2), there exists at least one x0 in [a,b] such that f(x0)=y.
Examples
-
Consider the function f(x)=cosx, in the interval [0,4π]. Then at the points π and 3π the function attains its minimum value (-1), while at the points 0, 2π, 4π it attains its maximum value (1): this shows that the points in the max-min theorem may not be unique.
-
Consider the function f(x)=x2, in the interval [-1,1]. The function attains its minimum value (0), at 0, its maximum value (1) at the points -1 and 1. If we consider the same function in the open interval ]-1,1[, it attains the same minimum value at 0, but no maximum value. This proves that closeness of the interval is fundamental.
-
Consider the function f(x)=1/x, in the interval [1,+∞[. It attains its maximum value (1) at 1, but no minimum value. This proves that unbounded intervals can't assure the existence of maxima and/or minima.
-
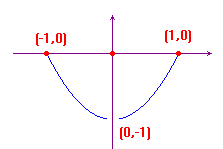
Consider the function f(x)=(x2-1)|sign(x)|. This function attains its maximum value (0) at the points -1, 0 and 1, but no minimum value. This proves that continuity is essential to assure the existence of maxima and/or minima. The picture here below reproduces the graph of this function.
-
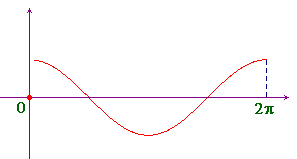
Consider the function f(x)=|sign(x)|cosx, in the interval [0,2π]. This function is not continuous in its domain (zero is the point where it is not continuous)), but it attains its maximum and minimum values (-1 and 1), as you can see in the picture here on the right. This proves that also non continuous functions can have maxima and minima: continuity is sufficient but not necessary.
-
Also Dirichlet's function
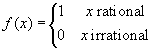 , though discontinuous at all points, has a maximum
and a minimum value: 0 and 1.
, though discontinuous at all points, has a maximum
and a minimum value: 0 and 1.
-
Consider the function f(x)=x2, in the whole natural domain, R. This function has a minimum value (0), but no maximum value: this proves that even if the domain is not a bounded interval, the function can have maxima and/or minima. In other words the condition that the interval is bounded is sufficient but not necessary.
An application of the intermediate value theorem to numerical analysis.
The intermediate value theorem suggests a very simple technique for finding approximations to solutions of equations. This technique is based on repeated application of the theorem. It is sometimes known as the Bisection technique, and is based on the simple observation that a non-zero real number must be positive or negative, but not both.
Suppose that a function is continuous in the compact interval
[a,b]. Suppose further that f(a)f(b)<0. Then the
equation
f(x)=0 has at least one solution in the
interval [a,b]. Calculate f(c), where
c=(a+b)/2 is the midpoint of the interval [a,b].
Exactly one of the following holds:
- If f(c)=0 we have found a solution of the equation f(x)=0, and the process ends.
- If f(a)f(c)<0, we repeat the steps above by considering the function f(x) in the interval [a,c].
- If f(b)f(c)<0, we repeat the steps above by considering the function f(x) in the interval [c,b].
If the process does not end, then on each application we have halved the length of the interval under consideration, and so we can approximate the solution as much as we want.
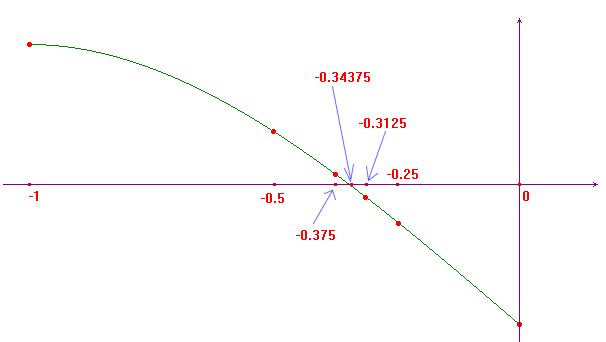
Example: Consider the function f(x)=x3-3x-1, in the interval [-1,0].
- We have f(-1)>0 and f(0)>0. As f(-0.5)>0, we consider the function in the interval [-0.5,0].
- As f(-0,25)<0, we consider the function in the interval [-0.5,-0.25].
- As f(-0.375)>0, we consider the function in the interval [-0.375,-0.25].
- As f(-0.3125)<0, we consider the function in the interval [-0.375,-0.3125].
- As f(-0.34375)<0, we consider the function in the interval [-0.375,-0.34375].
-
If we do not want to proceed we can conclude that a solution
of the equation f(x)=0 must be in the interval
[-0.375,-0.34375].
The picture below presents a graphical sketch of this process and shows that the middle point of the interval gets closer and closer to the desired solution of the equation.